题目内容
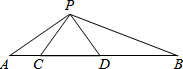 如图,点C、D在线段AB上,△PCD是等边三角形,且△ACP∽△PDB.
如图,点C、D在线段AB上,△PCD是等边三角形,且△ACP∽△PDB.(1)求∠APB的大小.
(2)说明线段AC、CD、BD之间的数量关系.
考点:相似三角形的性质,等边三角形的性质
专题:
分析:(1)由△ACP∽△PDB,可得∠APC=∠B,继而证得△ACP∽△APB,则可求得∠APB的大小.
(2)由△ACP∽△PDB,可得AC:PD=PC:BD,又由△PCD是等边三角形,即可得CD2=AC•BD.
(2)由△ACP∽△PDB,可得AC:PD=PC:BD,又由△PCD是等边三角形,即可得CD2=AC•BD.
解答:解:(1)∵△PCD是等边三角形,
∴∠PCD=60°,
∴∠ACP=120°,
∵△ACP∽△PDB,
∴∠APC=∠B,
∵∠A=∠A,
∴∠ACP∽∠APB,
∴∠APB=∠ACP=120°;
(2)∵△ACP∽△PDB,
∴AC:PD=PC:BD,
∴PD•PC=AC•BD,
∵△PCD是等边三角形,
∴PC=PD=CD,
∴CD2=AC•BD.
∴∠PCD=60°,
∴∠ACP=120°,
∵△ACP∽△PDB,
∴∠APC=∠B,
∵∠A=∠A,
∴∠ACP∽∠APB,
∴∠APB=∠ACP=120°;
(2)∵△ACP∽△PDB,
∴AC:PD=PC:BD,
∴PD•PC=AC•BD,
∵△PCD是等边三角形,
∴PC=PD=CD,
∴CD2=AC•BD.
点评:此题考查了相似三角形的判定与性质以及等边三角形的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
下列说法错误的是( )
| A、不等式-2x<8的解是x>-4 |
| B、不等式x<2的正整数解只有一个 |
| C、不等式x<5的整数解有无数个 |
| D、-4.5是不等式2x>-8的一个解 |
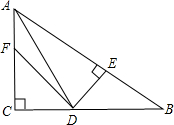 如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;
如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF; 已知:如图,AB∥CD,∠B=33°,∠E=12°,则∠D的度数为
已知:如图,AB∥CD,∠B=33°,∠E=12°,则∠D的度数为