题目内容
1.函数y=$\frac{\sqrt{1+x}}{x+3}$中,自变量x的取值范围是x≥-1.分析 根据二次根式的性质和分式的意义,被开方数大于等于0,可知:x+1≥0;分母不等于0,可知:x+3≠0,所以自变量x的取值范围就可以求出.
解答 解:根据题意得:x+1≥0且x+3≠0,
解得:x≥-1,
故答案为:x≥-1.
点评 本题考查了函数自变量的取值范围,使得分式和根号有意义的知识.函数自变量的范围一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数为非负数.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.一组数据2,0,1,x,3的平均数是2,则这组数据的方差是( )
| A. | 2 | B. | 4 | C. | 1 | D. | 3 |
13.计算$\frac{1}{x-1}$+$\frac{x}{1-x}$的结果是( )
| A. | x-1 | B. | 1-x | C. | 1 | D. | -1 |
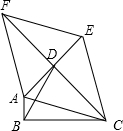 定义:只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个损矩形的直径,即损矩形外接圆的直径.如图,△ABC中,∠ABC=90°,以AC为一边向形外作菱形ACEF,点D是菱形ACEF对角线的交点,连接BD.若∠DBC=60°,∠ACB=15°,BD=2$\sqrt{3}$,则菱形ACEF的面积为12$\sqrt{3}$.
定义:只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个损矩形的直径,即损矩形外接圆的直径.如图,△ABC中,∠ABC=90°,以AC为一边向形外作菱形ACEF,点D是菱形ACEF对角线的交点,连接BD.若∠DBC=60°,∠ACB=15°,BD=2$\sqrt{3}$,则菱形ACEF的面积为12$\sqrt{3}$. 小华从家里到学校的路是一段平路和一段下坡路,假设他始终保持平路每分钟走60m,下坡路每分钟走80m,上坡路每分钟走40m,则他从家里到学校需10min,从学校到家里需15min.问:从小华家到学校的平路和下坡路各有多远?
小华从家里到学校的路是一段平路和一段下坡路,假设他始终保持平路每分钟走60m,下坡路每分钟走80m,上坡路每分钟走40m,则他从家里到学校需10min,从学校到家里需15min.问:从小华家到学校的平路和下坡路各有多远?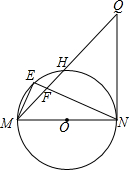 如图,MN是⊙O的直径,QN是⊙O的切线,连接MQ交⊙O于点H,E为$\widehat{MH}$上一点,连接ME,NE,NE交MQ于点F,且ME2=EF•EN.
如图,MN是⊙O的直径,QN是⊙O的切线,连接MQ交⊙O于点H,E为$\widehat{MH}$上一点,连接ME,NE,NE交MQ于点F,且ME2=EF•EN. 如图,点A在双曲线y=$\frac{k}{x}$上,AB⊥x轴于点B,且△AOB的面积是2,则k的值是-4.
如图,点A在双曲线y=$\frac{k}{x}$上,AB⊥x轴于点B,且△AOB的面积是2,则k的值是-4.