题目内容
8.(1)计算:2cos45°-(-$\frac{1}{4}$)-1-$\sqrt{8}$-(π-$\sqrt{3}$)0(2)解方程:$\frac{x+2}{x}$-$\frac{2}{{x}^{2}+2x}$=1.
分析 (1)分别根据0指数数幂的运算法则、负整数指幂的运算法则,数的开方法则及特殊角的三角函数值计算出各数,再根据实数混合运算的法则进行计算即可;
(2)先把分式方程化为整式方程求出x的值,再代入最减公分母进行检验即可.
解答 解:(1)原式=2×$\frac{\sqrt{2}}{2}$+4-2$\sqrt{2}$-1
=$\sqrt{2}$+4-2$\sqrt{2}$-1
=3-$\sqrt{2}$;
(2)方程两边同时乘以x(x+2)得,(x+2)2-2=x2+2x,
解得,x=-1,
经检验x=-1是原分式方程的解.
点评 本题考查的是实数的运算,熟知0指数数幂的运算法则、负整数指幂的运算法则,数的开方法则及特殊角的三角函数值是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.二次函数y=x2-|k|与正比例函数y=kx(k≠0)图象的位置关系为( )
| A. | 相离 | B. | 相切 | C. | 相交 | D. | 不能确定 |
3.下列四个数中,最小的数是( )
| A. | 0 | B. | 1 | C. | -$\frac{1}{2}$ | D. | -1 |
13.下列实数中是无理数的是( )
| A. | $\sqrt{4}$ | B. | $\root{3}{8}$ | C. | π0 | D. | sin45° |
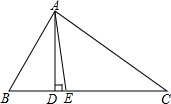 如图,在△ABC中,∠B>∠C,AD⊥BC,AE平分∠BAC,
如图,在△ABC中,∠B>∠C,AD⊥BC,AE平分∠BAC, 如图是每个面上都有一个汉字的正方体的一种侧面展开图,那么在原正方体的表面上,与汉字“美”相对的面上的汉字是( )
如图是每个面上都有一个汉字的正方体的一种侧面展开图,那么在原正方体的表面上,与汉字“美”相对的面上的汉字是( ) 已知直线y1=x+b与抛物线y2=-x2+ax+c的一个交点为(2,3),且x=1为该抛物线的对称轴.
已知直线y1=x+b与抛物线y2=-x2+ax+c的一个交点为(2,3),且x=1为该抛物线的对称轴.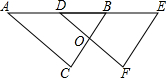 如图,△DEF是由△ABC经过平移得到的,若∠E=70°,∠A=33°,则∠ABC的度数是70°.
如图,△DEF是由△ABC经过平移得到的,若∠E=70°,∠A=33°,则∠ABC的度数是70°.