题目内容
18.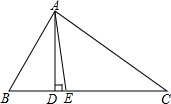 如图,在△ABC中,∠B>∠C,AD⊥BC,AE平分∠BAC,
如图,在△ABC中,∠B>∠C,AD⊥BC,AE平分∠BAC,(1)若∠B=80°,∠C=40°,求∠DAE的度数;
(2)若∠B=40°,∠C=30°,则∠DAE=5°;
(3)若∠B-∠C=40°,则∠DAE=20°;
(4)由(1)、(2)、(3)请猜想出∠DAE与∠B、∠C之间的关系为∠DAE=$\frac{1}{2}$(∠B-∠C).
分析 (1)根据三角形内角和得出∠BAC,再根据角平分线定义得出∠BAE,利用互余得出∠BAD,最后解答即可;
(2)根据三角形内角和得出∠BAC,再根据角平分线定义得出∠BAE,利用互余得出∠BAD,最后解答即可;
(3)根据三角形内角和得出∠BAC,再根据角平分线定义得出∠BAE,利用互余得出∠BAD,最后解答即可;
(4)由(1)(2)(3)推理可得三者关系.
解答 解:(1)∵∠B=80°,∠C=40°,
∴∠BAC=180°-80°-40°=60°,
∵AE平分∠BAC,
∴∠BAE=30°,
∵AD⊥BC,∠B=80°,
∴∠BAD=10°,
∴∠DAE=30°-10°=20°;
(2)∵∠B=40°,∠C=30°,
∴∠BAC=180°-40°-30°=110°,
∵AE平分∠BAC,
∴∠BAE=55°,
∵AD⊥BC,∠B=40°,
∴∠BAD=50°,
∴∠DAE=55°-50°=5°;
(3)∵∠B-∠C=40°,
∴∠BAC=180°-∠B-(∠B-40°)=140°-2∠B,
∵AE平分∠BAC,
∴∠BAE=70°-∠B,
∵AD⊥BC,
∴∠BAD=90°-∠B,
∴∠DAE=90°-∠B-(70°-∠B)=20°;
(4)由(1)和(2)(3)可得:∠DAE=$\frac{1}{2}$(∠B-∠C);
故答案为:(2)5°;(3)20°;(4)∠DAE=$\frac{1}{2}$(∠B-∠C).
点评 此题考查三角形内角和问题,关键是根据三角形内角和和角平分线的定义进行分析.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
13.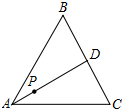 如图,P为等边△ABC的中线AD上一点,AD=3AP,在边AB、AC上分别取点M、N,使△PMN为以MN为底的等腰直角三角形,若AP=1+$\sqrt{3}$,则MN的长为( )
如图,P为等边△ABC的中线AD上一点,AD=3AP,在边AB、AC上分别取点M、N,使△PMN为以MN为底的等腰直角三角形,若AP=1+$\sqrt{3}$,则MN的长为( )
 如图,P为等边△ABC的中线AD上一点,AD=3AP,在边AB、AC上分别取点M、N,使△PMN为以MN为底的等腰直角三角形,若AP=1+$\sqrt{3}$,则MN的长为( )
如图,P为等边△ABC的中线AD上一点,AD=3AP,在边AB、AC上分别取点M、N,使△PMN为以MN为底的等腰直角三角形,若AP=1+$\sqrt{3}$,则MN的长为( )| A. | 2 | B. | 4+2$\sqrt{3}$ | C. | 2$\sqrt{2}$+$\sqrt{6}$ | D. | 4+2$\sqrt{3}$或2 |
10.重庆市奉节县以盛产脐橙而闻名,春节期间,达州市一水果批发经销商为满足市场需要,安排15辆汽车到奉节县装运A、B、C三种不同品质的脐橙120吨到达州销售,按计划15辆汽车都要装满县每辆汽车只能装同一种品质的脐橙,每种脐橙所用车辆都不少于3辆.
(1)设装运A种脐橙的车辆数为x辆,装运B种脐橙车辆数为y辆,根据下表提供的信息,求出y与x之间的函数关系式;
(2)在(1)条件下,求出该函数自变量x的取值范围,车辆的安排方案共有几种?请写出每种安排方案;
(3)为了减少脐橙积压,奉节县政府制定出台了促进脐橙销售的优惠政策,在外地运销客户原有获利不变的情况下,政府对外地运销商按每吨60元的标准实行运费补贴.若外地运销商要想所获利润W(元)最大,应采用哪种车辆安排方案?并求出利润W(元)的最大值?
(1)设装运A种脐橙的车辆数为x辆,装运B种脐橙车辆数为y辆,根据下表提供的信息,求出y与x之间的函数关系式;
| 脐橙品种 | A | B | C |
| 每辆汽车运载(吨) | 10 | 8 | 6 |
| 每吨脐橙所获利润(元) | 600 | 1000 | 800 |
(3)为了减少脐橙积压,奉节县政府制定出台了促进脐橙销售的优惠政策,在外地运销客户原有获利不变的情况下,政府对外地运销商按每吨60元的标准实行运费补贴.若外地运销商要想所获利润W(元)最大,应采用哪种车辆安排方案?并求出利润W(元)的最大值?
7.在四张完全相同的卡片上,分别画有平行四边形、菱形、等腰三角形、等腰梯形,现从中随机抽取一张,卡片上的图形恰好是中心对称图形的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
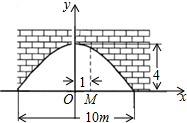 如图,有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为4m,跨度为10m.把它的截面边缘的图形放在如图所示的直角坐标系中.在对称轴右边1m处,桥洞离水面的高是$\frac{99}{25}$m.
如图,有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为4m,跨度为10m.把它的截面边缘的图形放在如图所示的直角坐标系中.在对称轴右边1m处,桥洞离水面的高是$\frac{99}{25}$m.