题目内容
9.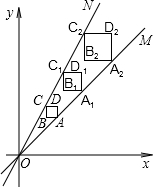 如图,正方形ABCD、正方形A1B1C1D1和正方形A2B2C2D2均位于平面直角坐标系的第一象限内,它们的边平行于x轴或y轴,其中点A,A1,A2在直线OM上,点C,C1,C2在直线ON上,O为坐标原点,已知点A的坐标为(3,3),正方形ABCD的边长为1.
如图,正方形ABCD、正方形A1B1C1D1和正方形A2B2C2D2均位于平面直角坐标系的第一象限内,它们的边平行于x轴或y轴,其中点A,A1,A2在直线OM上,点C,C1,C2在直线ON上,O为坐标原点,已知点A的坐标为(3,3),正方形ABCD的边长为1.(1)求直线ON的函数解析式;
(2)若点C1的横坐标为4,求正方形A1B1C1D1的边长;
(3)若正方形A2B2C2D2的边长为m,则点B2的坐标为(2m,3m).(用含字母m的代数式表示.
分析 (1)由A的坐标与正方形ABCD的边长,确定出B与C坐标,设直线ON解析式为y=kx,把C坐标代入求出k的值,即可确定出解析式;
(2)由C1的横坐标以及直线ON解析式,求出C1的纵坐标,得到C1的坐标,设正方形A1B1C1D1的边长为l,表示出B1与A1坐标,根据题意列出关于l的方程,求出方程的解得到l的值,即可确定出正方形A1B1C1D1的边长;
(3)根据题意得到A2B2=B2C2=m,根据A2在直线y=x上,设出A2坐标,进而表示出B2与C2,把C2坐标代入y=2x中表示出a,即可确定出B2的坐标.
解答 解:(1)∵A(3,3),正方形ABCD边长为1,
∴B(2,3),C(2,4),
设直线ON解析式为y=kx,
把C坐标代入得:k=2,
则直线ON的表达式为y=2x;
(2)∵点C1的横坐标为4,且在直线ON上,
∴C1坐标为(4,8),
设正方形A1B1C1D1的边长为l,
∴B1(4,8-l),A1(4+l,8-l),
由A的坐标为(3,3),得到直线OM解析式为y=x,
∵A1在直线OM上,
∴4+l=8-l,
解得:l=2,
则正方形A1B1C1D1的边长为2;
(3)依题意,A2B2=B2C2=m,
∵A2在直线y=x上,
设A2(a,a),可得B2(a-m,a),C2(a-m,a+m),
将C2代入直线y=2x中,得a+m=2(a-m),
解得:a=3m,
∴a-m=2m,即B2(2m,3m).
故答案为:(2m,3m)
点评 此题属于一次函数综合题,涉及的知识有:正方形的性质,待定系数法求一次函数解析式,坐标与图形性质,熟练掌握一次函数的性质是解本题的关键.

练习册系列答案
相关题目
1.(-2)3的值为( )
| A. | -8 | B. | -6 | C. | 6 | D. | 8 |
4.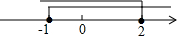 把某不等式组中两个不等式的解集表示在数轴上,如图所示,则这个不等式组可能是( )
把某不等式组中两个不等式的解集表示在数轴上,如图所示,则这个不等式组可能是( )
 把某不等式组中两个不等式的解集表示在数轴上,如图所示,则这个不等式组可能是( )
把某不等式组中两个不等式的解集表示在数轴上,如图所示,则这个不等式组可能是( )| A. | $\left\{\begin{array}{l}{x>-1}\\{x≤2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x≥-1}\\{x<2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x≥-1}\\{x≤2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x<-1}\\{x≥2}\end{array}\right.$ |
16.$\root{3}{-8}$等于( )
| A. | 2 | B. | 2$\sqrt{3}$ | C. | -$\frac{1}{2}$ | D. | -2 |



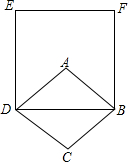 如图,菱形ABCD中,∠ABC=60°,AB=4,则以BD为边长的正方形BDEF的面积为48.
如图,菱形ABCD中,∠ABC=60°,AB=4,则以BD为边长的正方形BDEF的面积为48.