题目内容
18.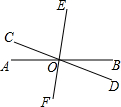 如图,直线AB,CD,EF相交于点O,∠AOD=160°,∠BOE=4∠AOC.
如图,直线AB,CD,EF相交于点O,∠AOD=160°,∠BOE=4∠AOC.(1)写出∠AOC,∠AOD的对顶角;
(2)求∠BOE的度数;
(3)求证:OE平分∠BOC.
分析 (1)根据对顶角:有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角进行分析即可;
(2)首先设∠AOC=x°,则∠BOE=4x°,根据邻补角互补可得∠AOC+∠AOD=180°,进而可得方程x+160=180,再解即可得到x的值,进而可得∠EOC的角度;
(3)根据对顶角相等可得∠BOC的度数,再根据角的和差关系可得∠COE的度数,从而可得结论.
解答 (1)解:∠AOC的对顶角是∠BOD,∠AOD的对顶角是∠BOC;
(2)解:设∠AOC=x°,则∠BOE=4x°,
∵∠AOC+∠AOD=180°,
∴x+160=180,
解得:x=20,
∴∠BOE=80°;
(3)证明:∵∠AOD=160°,
∴∠BOC=160°,
∵∠BOE=80°,
∴∠COE=160°-80°=80°,
∴OE平分∠BOC.
点评 此题主要考查了邻补角、对顶角,以及角平分线,关键是掌握邻补角互补,对顶角相等.

练习册系列答案
相关题目
9.计算(-$\frac{1}{2}$)2016+(-$\frac{1}{2}$)2017得( )
| A. | -$\frac{1}{{2}^{2017}}$ | B. | -$\frac{1}{{2}^{2016}}$ | C. | ($\frac{1}{2}$)2017 | D. | ($\frac{1}{2}$)2016 |
13.下列各组二次根式,经化简后可以合并的是( )
| A. | $\sqrt{12}$与$\sqrt{24}$ | B. | $\sqrt{18}$与$\sqrt{24}$ | C. | $\sqrt{8}$与$\sqrt{18}$ | D. | $\sqrt{45}$与$\sqrt{12}$ |
7. 如图所示,已知∠3=∠4,若要使∠1=∠2,则需( )
如图所示,已知∠3=∠4,若要使∠1=∠2,则需( )
 如图所示,已知∠3=∠4,若要使∠1=∠2,则需( )
如图所示,已知∠3=∠4,若要使∠1=∠2,则需( )| A. | ∠1=∠3 | B. | ∠2=∠3 | C. | AB∥CD | D. | ∠1=∠4 |
8.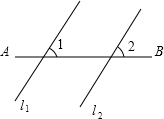 如图,将直线l1沿AB的方向平移得到l2,若∠1=40°,则∠2=( )
如图,将直线l1沿AB的方向平移得到l2,若∠1=40°,则∠2=( )
 如图,将直线l1沿AB的方向平移得到l2,若∠1=40°,则∠2=( )
如图,将直线l1沿AB的方向平移得到l2,若∠1=40°,则∠2=( )| A. | 40° | B. | 50° | C. | 90° | D. | 140° |
 如图,已知直线AB∥CD,BC∥DE,若∠B=60°,则∠D=120°.
如图,已知直线AB∥CD,BC∥DE,若∠B=60°,则∠D=120°.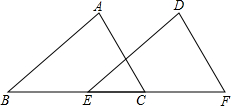 已知,如图,AC=DF,AC∥DF,BE=CF,请写出△ABC≌△DEF的理由.
已知,如图,AC=DF,AC∥DF,BE=CF,请写出△ABC≌△DEF的理由. 分别在直角坐标系中描出点(1)(0,0),(5,4),(3,0),(5,1)(5,-1),(3,0),(4,-2),(0,0);按描点的顺序连线.
分别在直角坐标系中描出点(1)(0,0),(5,4),(3,0),(5,1)(5,-1),(3,0),(4,-2),(0,0);按描点的顺序连线.