题目内容
5．（1）计算：$\root{3}{8}$-$\sqrt{\frac{4}{25}}$；（2）解方程组：$\left\{\begin{array}{l}{3x-2y=0}\\{x-y=1}\end{array}\right.$．
分析 （1）原式利用立方根及算术平方根定义计算即可得到结果；
（2）方程组利用加减消元法求出解即可．
解答 解：（1）原式=2-$\frac{2}{5}$=$\frac{8}{5}$；
（2）$\left\{\begin{array}{l}{3x-2y=0①}\\{x-y=1②}\end{array}\right.$，
①-②×2得：x=-2，
把x=-2代入②得：y=-3，
则方程组的解为$\left\{\begin{array}{l}{x=-2}\\{y=-3}\end{array}\right.$．
点评 此题考查了实数的运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
16．
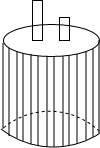如图，两根铁棒直立于桶底水平的木桶，在桶中加入水后，一根露出水面的长度是它的$\frac{1}{3}$，另一根露出水面的长度是它的$\frac{1}{5}$．两根铁棒长度之和为220cm，求此时木桶中水的深度．如果设一根铁棒长xcm，另一根铁棒长ycm，则可列方程组为（ ）
如图，两根铁棒直立于桶底水平的木桶，在桶中加入水后，一根露出水面的长度是它的$\frac{1}{3}$，另一根露出水面的长度是它的$\frac{1}{5}$．两根铁棒长度之和为220cm，求此时木桶中水的深度．如果设一根铁棒长xcm，另一根铁棒长ycm，则可列方程组为（ ）| A． | $\left\{\begin{array}{l}{x+y=220}\\{\frac{1}{3}x=\frac{1}{5}y}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x+y=220}\\{（1-\frac{1}{3}）x=（1-\frac{1}{5}）y}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{x+y=220}\\{220-\frac{1}{3}x=220-\frac{1}{5}y}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x+y=220}\\{3x=5y}\end{array}\right.$ |
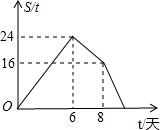某农资销售部连续8天调进一批化肥进行销售，在开始调进化肥的第7天开始销售．若进货期间每天调入化肥的吨数与销售期间每天销售化肥的吨数都保持不变，这个销售部的化肥存量S（单位：吨）与时间t（单位：天）之间的函数关系如图所示，则该销售部这次化肥销售活动（从开始进货到销售完毕）所用时间是10天．
20．下列计算结果正确的是（ ）
| A． | $\sqrt{2}+\sqrt{3}$=$\sqrt{5}$ | B． | 3$\sqrt{2}$-$\sqrt{2}$=3 | C． | $\sqrt{2}×\sqrt{5}$=$\sqrt{10}$ | D． | $\frac{\sqrt{2}}{\sqrt{5}}$=5$\sqrt{10}$ |
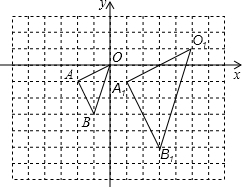在如图的方格中，△OAB的顶点坐标分别为O（0，0）、A（-2，-1）、B（-1，-3），△O1A1B1与△OAB是关于点P为位似中心的位似图形．