题目内容
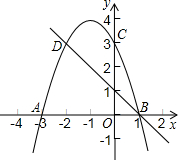 如图,二次函数的图象与x轴相交于A(-3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
如图,二次函数的图象与x轴相交于A(-3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.(1)求D点坐标;
(2)求二次函数的解析式;
(3)根据图象直接写出使一次函数值小于二次函数值的x的取值范围.
考点:抛物线与x轴的交点,待定系数法求二次函数解析式,二次函数与不等式(组)
专题:
分析:(1)利用点C、D是二次函数图象上的一对对称点,可得出D点的坐标;
(2)设该抛物线的解析式为y=a(x+3)(x-1)(a≠0),然后将点C的坐标代入来求a的值;
(3)在坐标系中利用x取相同值,比较出对应值的大小,从而确定,两函数的大小关系.
(2)设该抛物线的解析式为y=a(x+3)(x-1)(a≠0),然后将点C的坐标代入来求a的值;
(3)在坐标系中利用x取相同值,比较出对应值的大小,从而确定,两函数的大小关系.
解答:解:(1)∵抛物线的对称轴是x=-1,而C、D关于直线x=-1对称,
∴D(-2,3);
(2)设该抛物线的解析式为y=a(x+3)(x-1)(a≠0),
把C(0,3)代入,得
3=a(0+3)(0-1),
解得 a=-1,
所以该抛物线的解析式为y=-(x+3)(x-1)=-x2-2x+3,
即y=-x2-2x+3;
(3)根据图象知,一次函数值小于二次函数值的x的取值范围是:-2<x<1.
∴D(-2,3);
(2)设该抛物线的解析式为y=a(x+3)(x-1)(a≠0),
把C(0,3)代入,得
3=a(0+3)(0-1),
解得 a=-1,
所以该抛物线的解析式为y=-(x+3)(x-1)=-x2-2x+3,
即y=-x2-2x+3;
(3)根据图象知,一次函数值小于二次函数值的x的取值范围是:-2<x<1.
点评:此题主要考查了抛物线与x轴的交点,二次函数的对称性,以及待定系数法求二次函数解析式和利用自变量的取值范围确定函数值大小关系,题目难度不大,非常典型.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
 如图,数轴的单位长度为1,如果B、C表示的数的和为2,那么A、D表示的数的和是( )
如图,数轴的单位长度为1,如果B、C表示的数的和为2,那么A、D表示的数的和是( )| A、5 | B、4 | C、3 | D、2 |
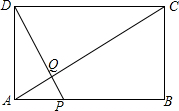 如图,矩形ABCD中,AB=10,BC=5,点P为AB边上一点,DP交AC于点Q.
如图,矩形ABCD中,AB=10,BC=5,点P为AB边上一点,DP交AC于点Q.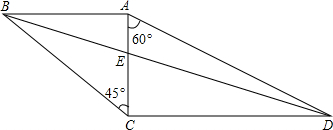 如图,将三角尺ABC、ACD摆放在一起,设BD交AC于点E,则△ABE∽
如图,将三角尺ABC、ACD摆放在一起,设BD交AC于点E,则△ABE∽ 如图,已知第一象限内的点A在反比例函数y=
如图,已知第一象限内的点A在反比例函数y=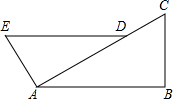 已知:如图,在Rt△ABC中,∠B=90°,AE⊥CA,且AE=BC,点D在AC上,且AD=AB,求证:DE∥AB.
已知:如图,在Rt△ABC中,∠B=90°,AE⊥CA,且AE=BC,点D在AC上,且AD=AB,求证:DE∥AB.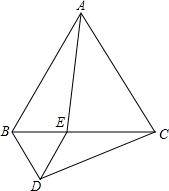 如图,等边三角形ABC的边长为2,点E是边BC上一动点(不与点B、C重合),以BE为边在BC的下方作等边三角形BDE,连接AE、CD.
如图,等边三角形ABC的边长为2,点E是边BC上一动点(不与点B、C重合),以BE为边在BC的下方作等边三角形BDE,连接AE、CD.