题目内容
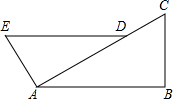已知：如图，在Rt△ABC中，∠B=90°，AE⊥CA，且AE=BC，点D在AC上，且AD=AB，求证：DE∥AB．考点：全等三角形的判定与性质,平行线的判定
专题：证明题
分析：由AE⊥CA得出∠EAD=90°=∠CBA，再根据已知条件AB=AD，BC=AE，即可证出△BCA≌△AED（SAS），得出∠CAB=∠EDA，因此DE∥AB．
解答：证明：∵AE⊥CA，
∴∠EAD=90°，
∵∠CBA=90°，
∴∠CBA=∠EAD，
在△BCA和△AED中，
，
∴△BCA≌△AED（SAS），
∴∠CAB=∠EDA，
∴DE∥AB．
∴∠EAD=90°，
∵∠CBA=90°，
∴∠CBA=∠EAD，
在△BCA和△AED中，
|
∴△BCA≌△AED（SAS），
∴∠CAB=∠EDA，
∴DE∥AB．
点评：本题考查了全等三角形的判定与性质和平行线的判定方法；证明三角形全等是解决问题的关键．
练习册系列答案
阅读快车系列答案
相关题目
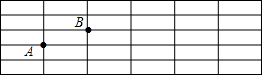如图，在长方形网格中，每个小长方形的长为3，宽为1，A、B两点在网格格点上．若点C也在网格格点上，以A、B、C为顶点的三角形面积为3，则满足条件的点C有（ ）
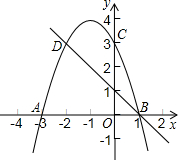如图，二次函数的图象与x轴相交于A（-3，0）、B（1，0）两点，与y轴相交于点C（0，3），点C、D是二次函数图象上的一对对称点，一次函数的图象过点B、D．
如图，Rt△ABC中∠C=90°，AD•AC=AE•AB，求证：DE⊥AB．四个角都相等，且邻边相等的四边形是（ ）
| A、平行四边形 | B、菱形 |
| C、矩形 | D、正方形 |
如图：已知平行四边形ABCD中，K是BC上一点，且| BK |
| KC |
| 3 |
| 4 |
| BE |
| ED |
A、
| ||
B、
| ||
C、
| ||
D、
|
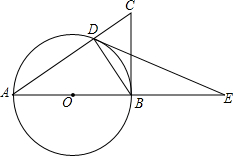如图，Rt△ABC中，∠ABC=90°，以AB为直径作⊙O，交AC于点D，点E是AB延长线上的一点，且∠BDE=∠A．