题目内容
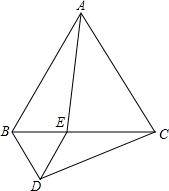 如图,等边三角形ABC的边长为2,点E是边BC上一动点(不与点B、C重合),以BE为边在BC的下方作等边三角形BDE,连接AE、CD.
如图,等边三角形ABC的边长为2,点E是边BC上一动点(不与点B、C重合),以BE为边在BC的下方作等边三角形BDE,连接AE、CD.(1)在运动的过程中,AE与CD有何数量关系?请说明理由.
(2)当BE=1时,求∠BDC的度数.
考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:(1)如图,证明△ABE≌△CBD,即可解决问题.
(2)证明AE⊥BC;证明∠BDC=∠AEB,即可解决问题.
(2)证明AE⊥BC;证明∠BDC=∠AEB,即可解决问题.
解答: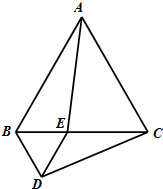 解:(1)AE=CD;理由如下:
解:(1)AE=CD;理由如下:
如图,∵△ABC和△BDE等边三角形
∴AB=BC,BE=BD,∠ABC=∠EBD=60°;
在△ABE与△CBD中,
,
∴△ABE≌△CBD(SAS),
∴AE=CD.
(2)∵BE=1,BC=2
∴E为BC的中点;
又∵等边三角形△ABC,
∴AE⊥BC;
由(1)知△ABE≌△CBD,
∴∠BDC=∠AEB=90°.
 解:(1)AE=CD;理由如下:
解:(1)AE=CD;理由如下:如图,∵△ABC和△BDE等边三角形
∴AB=BC,BE=BD,∠ABC=∠EBD=60°;
在△ABE与△CBD中,
|
∴△ABE≌△CBD(SAS),
∴AE=CD.
(2)∵BE=1,BC=2
∴E为BC的中点;
又∵等边三角形△ABC,
∴AE⊥BC;
由(1)知△ABE≌△CBD,
∴∠BDC=∠AEB=90°.
点评:该题主要考查了全等三角形的判定及其性质的应用问题;解题的关键是观察图形,准确找出图形中隐含的等量关系、全等关系.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 如图:已知平行四边形ABCD中,K是BC上一点,且
如图:已知平行四边形ABCD中,K是BC上一点,且| BK |
| KC |
| 3 |
| 4 |
| BE |
| ED |
A、
| ||
B、
| ||
C、
| ||
D、
|
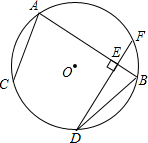 如图,已知AB、AC是⊙O的弦,D为弧BC的中点,弦DF⊥AB于E,AC=2,AB=3,则BE的长为( )
如图,已知AB、AC是⊙O的弦,D为弧BC的中点,弦DF⊥AB于E,AC=2,AB=3,则BE的长为( )| A、1 | ||
B、
| ||
C、
| ||
D、
|
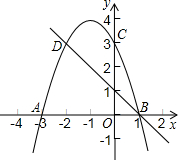 如图,二次函数的图象与x轴相交于A(-3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
如图,二次函数的图象与x轴相交于A(-3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.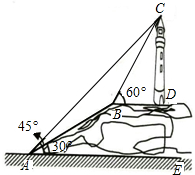 如图,某教学学习小组为了测量山顶上一古灯塔的高度CD,他们在山脚下的点A处测得塔顶C处的仰角为45°,沿着坡角为30°的登山梯AB向上走200米到达山顶B处后,测得塔顶C处的仰角为60°,已知点B与底部D在同一水平线上.
如图,某教学学习小组为了测量山顶上一古灯塔的高度CD,他们在山脚下的点A处测得塔顶C处的仰角为45°,沿着坡角为30°的登山梯AB向上走200米到达山顶B处后,测得塔顶C处的仰角为60°,已知点B与底部D在同一水平线上.
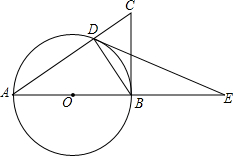 如图,Rt△ABC中,∠ABC=90°,以AB为直径作⊙O,交AC于点D,点E是AB延长线上的一点,且∠BDE=∠A.
如图,Rt△ABC中,∠ABC=90°,以AB为直径作⊙O,交AC于点D,点E是AB延长线上的一点,且∠BDE=∠A. 如图,A、D是直线l1上两点,B、C是直线l2上两点,且AB⊥BC,CD⊥AD.
如图,A、D是直线l1上两点,B、C是直线l2上两点,且AB⊥BC,CD⊥AD.