题目内容
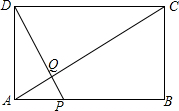 如图,矩形ABCD中,AB=10,BC=5,点P为AB边上一点,DP交AC于点Q.
如图,矩形ABCD中,AB=10,BC=5,点P为AB边上一点,DP交AC于点Q.(1)求证:△APQ∽△CDQ;
(2)当PD⊥AC时,求线段PA的长度.
考点:相似三角形的判定与性质,矩形的性质
专题:
分析:(1)根据矩形的性质,可得出AB∥CD,从而得出∠PAQ=∠DCQ,∠QPA=∠QDC,利用两角对应相等的三角形相似得出结论;
(2)由PD⊥AC,得∠ACD+∠PDC=90°,从而得出∠ACD=∠PDA,可证明△ADC∽△PAD,由相似比得出PA的长.
(2)由PD⊥AC,得∠ACD+∠PDC=90°,从而得出∠ACD=∠PDA,可证明△ADC∽△PAD,由相似比得出PA的长.
解答:(1)证明:∵四边形ABCD是矩形,
∴AB∥CD,
∴∠PAQ=∠DCQ,∠QPA=∠QDC,
∴△APQ∽△CDQ.
(2)解:∵PD⊥AC,
∴∠ACD+∠PDC=90°,
∵∠PDA+∠PDC=90°,
∴∠ACD=∠PDA,
∵∠ADC+∠PAD=90°,
∴△ADC∽△PAD,
∴
=
,
∴
=
,
∴PA=2.5.
∴AB∥CD,
∴∠PAQ=∠DCQ,∠QPA=∠QDC,
∴△APQ∽△CDQ.
(2)解:∵PD⊥AC,
∴∠ACD+∠PDC=90°,
∵∠PDA+∠PDC=90°,
∴∠ACD=∠PDA,
∵∠ADC+∠PAD=90°,
∴△ADC∽△PAD,
∴
| AD |
| PA |
| DC |
| AD |
∴
| 5 |
| PA |
| 10 |
| 5 |
∴PA=2.5.
点评:本题考查了相似三角形的判定和性质以及矩形的性质,综合性强,难度不大.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
一次数学测试后,随机抽取6名学生成绩如下:86,85,88,80,88,95,关于这组数据说法错误的是( )
| A、极差是15 |
| B、众数是88 |
| C、中位数是86 |
| D、平均数是87 |
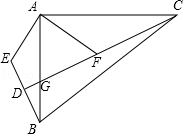 如图,在△ABC中,∠BAC=90°,∠EAF=90°,AB•AF=AC•AE.连接CF并延长CF交AB于点G,交BE于点D.
如图,在△ABC中,∠BAC=90°,∠EAF=90°,AB•AF=AC•AE.连接CF并延长CF交AB于点G,交BE于点D. 已知∠AOB=40°,∠AOB的余角为∠AOC,∠AOB的补角为∠BOD,OM平分∠AOC,ON平分∠BOD.
已知∠AOB=40°,∠AOB的余角为∠AOC,∠AOB的补角为∠BOD,OM平分∠AOC,ON平分∠BOD.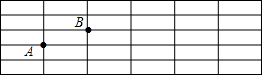 如图,在长方形网格中,每个小长方形的长为3,宽为1,A、B两点在网格格点上.若点C也在网格格点上,以A、B、C为顶点的三角形面积为3,则满足条件的点C有( )
如图,在长方形网格中,每个小长方形的长为3,宽为1,A、B两点在网格格点上.若点C也在网格格点上,以A、B、C为顶点的三角形面积为3,则满足条件的点C有( )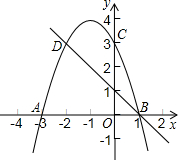 如图,二次函数的图象与x轴相交于A(-3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
如图,二次函数的图象与x轴相交于A(-3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.