题目内容
3.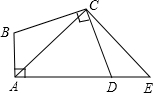 如图,在四边形ABCD中,∠A=∠BCD=90°,BC=CD.延长AD到E点,使DE=AB.
如图,在四边形ABCD中,∠A=∠BCD=90°,BC=CD.延长AD到E点,使DE=AB.(1)求证:∠ABC=∠EDC;
(2)连接AC,求证:AC=CE.
分析 (1)根据等角的补角相等即可证明;
(2)由BC=DC,∠ABC=∠EDC,AB=DE,根据SAS即可证明△CDE≌△CBA.
解答 (1)证明:∵∠A=∠BCD=90°
∴∠ABC+∠ADC=180°,∠ADC+∠CDE=180°,
∴∠ABC=∠EDC,
(2)解:
在△ABC和△EDC中,
$\left\{\begin{array}{l}{BC=DC}\\{∠ABC=∠EDC}\\{AB=DE}\end{array}\right.$
∴△CDE≌△CBA(SAS),
∴AC=CE
点评 本题考查全等三角形的判定和性质、等角的补角相等等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
13. 如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为点D,E,AD与BE交于点F,BF=AC,∠ABE=22°,∠CAD的度数是( )
如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为点D,E,AD与BE交于点F,BF=AC,∠ABE=22°,∠CAD的度数是( )
 如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为点D,E,AD与BE交于点F,BF=AC,∠ABE=22°,∠CAD的度数是( )
如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为点D,E,AD与BE交于点F,BF=AC,∠ABE=22°,∠CAD的度数是( )| A. | 23° | B. | 22° | C. | 32° | D. | 33° |
18.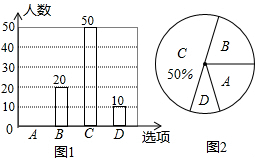 共享单车近日成为市民新宠,越来越多的居民选择共享单车作为出行的交通工具,某中学课外兴趣小组为了了解某小区居民每周使用共享单车时间的情况,随机抽取了该小区部分使用共享单车的居民进行调查(问卷调查表如图所示),并用调查结果绘制了图1、图2两幅每周使用共享单车时间的人数统计图(均不完整),请根据统计图解答以下问题:
共享单车近日成为市民新宠,越来越多的居民选择共享单车作为出行的交通工具,某中学课外兴趣小组为了了解某小区居民每周使用共享单车时间的情况,随机抽取了该小区部分使用共享单车的居民进行调查(问卷调查表如图所示),并用调查结果绘制了图1、图2两幅每周使用共享单车时间的人数统计图(均不完整),请根据统计图解答以下问题:
每周使用共享单车的时间问卷调查表
您好!这是一份关于您平均每周使用共享单车时间的问卷调查表,请在表格中选择一项符合您使用时间的选项,在其后空格内打“√”,非常感谢您的合作.
(1)本次接受问卷调查的共有100人;在扇形统计图中“D”选项所占的百分比为10%;
(2)扇形统计图中,“B”选项所对应扇形圆心角为72度;
(3)请补全条形统计图;
(4)若该小区共有1000名居民,请你估计该小区使用共享单车的时间在“A”选项的有多少人?
 共享单车近日成为市民新宠,越来越多的居民选择共享单车作为出行的交通工具,某中学课外兴趣小组为了了解某小区居民每周使用共享单车时间的情况,随机抽取了该小区部分使用共享单车的居民进行调查(问卷调查表如图所示),并用调查结果绘制了图1、图2两幅每周使用共享单车时间的人数统计图(均不完整),请根据统计图解答以下问题:
共享单车近日成为市民新宠,越来越多的居民选择共享单车作为出行的交通工具,某中学课外兴趣小组为了了解某小区居民每周使用共享单车时间的情况,随机抽取了该小区部分使用共享单车的居民进行调查(问卷调查表如图所示),并用调查结果绘制了图1、图2两幅每周使用共享单车时间的人数统计图(均不完整),请根据统计图解答以下问题:每周使用共享单车的时间问卷调查表
您好!这是一份关于您平均每周使用共享单车时间的问卷调查表,请在表格中选择一项符合您使用时间的选项,在其后空格内打“√”,非常感谢您的合作.
| 选项 | 使用时间t(小时) | |
| A | 0<t≤2 | |
| B | 2<t≤2.5 | |
| C | 2.5<t≤3 | |
| D | t>3 |
(2)扇形统计图中,“B”选项所对应扇形圆心角为72度;
(3)请补全条形统计图;
(4)若该小区共有1000名居民,请你估计该小区使用共享单车的时间在“A”选项的有多少人?
15.下列计算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 2$\sqrt{3}$×3$\sqrt{3}$=6$\sqrt{3}$ | C. | ($\sqrt{3}-\sqrt{2}$)×($\sqrt{3}+\sqrt{2}$)=1 | D. | ($\sqrt{3}+\sqrt{2}$)2=3+2=5 |
 如图,在△ABC中,高BF、CE相交于点H.
如图,在△ABC中,高BF、CE相交于点H. 如图.在矩形ABCD中.AB=6.BC=8.点A在直线1上,AD与直线1相交所得的锐角为60°,点F在直线1上.AF=8.EF⊥直线1.垂足为点F.且EF=6.以EF为直径.在EF的左侧作半圆O.点M是半圆O上任一点.
如图.在矩形ABCD中.AB=6.BC=8.点A在直线1上,AD与直线1相交所得的锐角为60°,点F在直线1上.AF=8.EF⊥直线1.垂足为点F.且EF=6.以EF为直径.在EF的左侧作半圆O.点M是半圆O上任一点.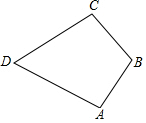 如图,在四边形ABCD中,已知AB=CB,AD=CD,∠ABC=120°,∠ADC=50°,求∠A和∠C的度数.
如图,在四边形ABCD中,已知AB=CB,AD=CD,∠ABC=120°,∠ADC=50°,求∠A和∠C的度数.


