题目内容
14. 如图,在△ABC中,高BF、CE相交于点H.
如图,在△ABC中,高BF、CE相交于点H.(1)写出两对图中的相似三角形;
(2)连接EF,①AB•AE=AC•AF成立吗?为什么?②$\frac{EF}{BC}$=$\frac{AF}{AB}$成立吗?为什么?
分析 (1)直接利用相似三角形的判定方法得出相似三角形;
(2)①利用△AEC∽△ABF,得出AB•AE=AC•AF成立;
②首先得出△AEF∽△ACB,进而得出$\frac{EF}{BC}$=$\frac{AF}{AB}$成立.
解答 解:(1)△AEC∽△ABF,△BEH∽△CFH;
(2)①AB•AE=AC•AF成立,
理由:∵△AEC∽△ABF,
∴$\frac{AE}{AF}$=$\frac{AC}{AB}$,
∴AB•AE=AC•AF;
②$\frac{EF}{BC}$=$\frac{AF}{AB}$成立,
理由:∵$\frac{AE}{AF}$=$\frac{AC}{AB}$,
∴$\frac{AE}{AC}$=$\frac{AF}{AB}$,
又∵∠A=∠A,
∴△AEF∽△ACB,
∴$\frac{EF}{BC}$=$\frac{AF}{AB}$.
点评 此题主要考查了相似三角形的判定与性质,正确掌握相似三角形的判定方法是解题关键.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
19.下列说法中正确的是( )
| A. | 不在同一条直线上的三个点确定一个圆 | |
| B. | 相等的圆心角所对的弧相等 | |
| C. | 平分弦的直径垂直于弦 | |
| D. | 在同圆或等圆中,相等的弦所对的圆周角相等 |
 已知二次函数y=ax2+bx+c的图象如图所示,则在①a<0,②b>0,③c<0,④b2-4ac>0中错误的个数为( )
已知二次函数y=ax2+bx+c的图象如图所示,则在①a<0,②b>0,③c<0,④b2-4ac>0中错误的个数为( )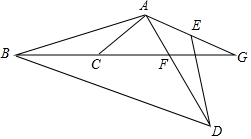 如图所示,AE=AC,AD=AB,∠GAC=∠BAD=110°,∠ACB=130°,求∠G的度数.
如图所示,AE=AC,AD=AB,∠GAC=∠BAD=110°,∠ACB=130°,求∠G的度数.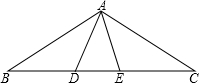 如图,在△ABC中,AD=AE,BD=CE,∠ADB=∠AEC,那么△ABD≌△ACE,△ABE≌ACD..
如图,在△ABC中,AD=AE,BD=CE,∠ADB=∠AEC,那么△ABD≌△ACE,△ABE≌ACD..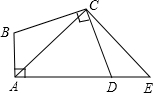 如图,在四边形ABCD中,∠A=∠BCD=90°,BC=CD.延长AD到E点,使DE=AB.
如图,在四边形ABCD中,∠A=∠BCD=90°,BC=CD.延长AD到E点,使DE=AB.


