题目内容
13. 如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为点D,E,AD与BE交于点F,BF=AC,∠ABE=22°,∠CAD的度数是( )
如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为点D,E,AD与BE交于点F,BF=AC,∠ABE=22°,∠CAD的度数是( )| A. | 23° | B. | 22° | C. | 32° | D. | 33° |
分析 求出△DBF≌△DAC,根据全等三角形的性质得出AD=BD,求出∠ABD=∠DAB=45°,即可得出答案.
解答 解:∵AD⊥BC,BE⊥AC,
∴∠BDF=∠ADC=90°,∠BEC=∠ADC=90°,
∴∠DAC+∠C=90°,∠DBF+∠C=90∴,
∴∠DBF=∠DAC,
在△DBF和△DAC中
$\left\{\begin{array}{l}{∠DBF=∠DAC}\\{∠BDF=∠ADC}\\{BF=AC}\end{array}\right.$
∴△DBF≌△DAC,
∴AD=BD,
∵∠ADB=90°,
∴∠ABD=∠DAB=45°,
∵∠ABE=22°,
∴∠CAD=∠DBF=∠ABD-∠ABE=45°-22°=23°,
故选A.
点评 本题考查了全等三角形的判定和性质,能灵活运用全等三角形的判定和性质定理进行推理是解此题的关键.

练习册系列答案
相关题目
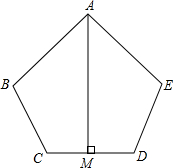 如图,在五边形ABCDE中,∠B=∠E,AB=AE,BC=ED,AM⊥CD,CM=3,求CD的长.
如图,在五边形ABCDE中,∠B=∠E,AB=AE,BC=ED,AM⊥CD,CM=3,求CD的长. 已知二次函数y=ax2+bx+c的图象如图所示,则在①a<0,②b>0,③c<0,④b2-4ac>0中错误的个数为( )
已知二次函数y=ax2+bx+c的图象如图所示,则在①a<0,②b>0,③c<0,④b2-4ac>0中错误的个数为( )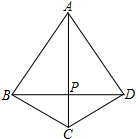 如图,四边形ABCD中,AB=AD,BC=CD,连结AC、BD交于点P,求证:AC⊥BD.
如图,四边形ABCD中,AB=AD,BC=CD,连结AC、BD交于点P,求证:AC⊥BD.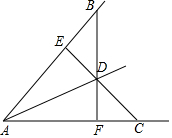 如图,BD=CD,BF⊥AC于F,CE⊥AB于E.求证:点D在∠BAC的角平分线上.
如图,BD=CD,BF⊥AC于F,CE⊥AB于E.求证:点D在∠BAC的角平分线上. 如图,在等腰三角形ABC中AB=AC,AD⊥BC点D,BE⊥AC于点E,AD与BE交于点P,BP=3,PE=1,求三角形BDP的面积.
如图,在等腰三角形ABC中AB=AC,AD⊥BC点D,BE⊥AC于点E,AD与BE交于点P,BP=3,PE=1,求三角形BDP的面积.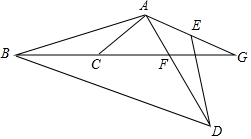 如图所示,AE=AC,AD=AB,∠GAC=∠BAD=110°,∠ACB=130°,求∠G的度数.
如图所示,AE=AC,AD=AB,∠GAC=∠BAD=110°,∠ACB=130°,求∠G的度数.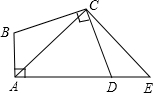 如图,在四边形ABCD中,∠A=∠BCD=90°,BC=CD.延长AD到E点,使DE=AB.
如图,在四边形ABCD中,∠A=∠BCD=90°,BC=CD.延长AD到E点,使DE=AB.