题目内容
4.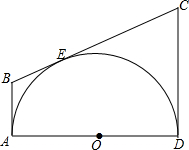 如图所示,AD为半圆O的直径,AB,CD与半圆O相切于A,D两点,BC与半圆O相切于点E.若AB=4,CD=9,则半圆O的直径是多少?
如图所示,AD为半圆O的直径,AB,CD与半圆O相切于A,D两点,BC与半圆O相切于点E.若AB=4,CD=9,则半圆O的直径是多少?
分析 根据AB,CD与半圆O相切于A,D两点,于是得到∠BAD=90°,∠ADC=90°,又BC与圆O相切于点E,且AB=4,CD=9,求得BE=AB=4,CE=CD=9,于是得到BC=BE+EC=13,过B作BF⊥DC于F点,则四边形ABFD为矩形,根据矩形的性质得到AB=DF=4,求出FC=5,在Rt△CFB中,根据勾股定理得到BF=$\sqrt{B{C}^{2}-C{F}^{2}}$=12,即可得到结论.
解答  解:∵AB,CD与半圆O相切于A,D两点,∴∠BAD=90°,
解:∵AB,CD与半圆O相切于A,D两点,∴∠BAD=90°,
∴∠ADC=90°,
又BC与圆O相切于点E,且AB=4,CD=9,
∴BE=AB=4,CE=CD=9,
∴BC=BE+EC=13,
过B作BF⊥DC于F点,则四边形ABFD为矩形,
∴AB=DF=4,
∴FC=5,
在Rt△CFB中,根据勾股定理得:BF=$\sqrt{B{C}^{2}-C{F}^{2}}$=12,
∴AD=BF=12.
∴半圆O的直径是12.
点评 此题考查了切线的判定与性质,切线长定理,勾股定理,梯形的面积公式,以及矩形的判定与性质,熟练掌握定理及性质是解本题的关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
14.已知一个数的倒数的绝对值等于这个数的相反数,则这个数是( )
| A. | 1 | B. | 0 | C. | -1或1 | D. | -1 |
 如图,将6个相连的正方形分割成8个面积相等的图形,怎么分?画出分割线.
如图,将6个相连的正方形分割成8个面积相等的图形,怎么分?画出分割线.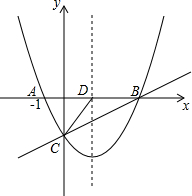 如图,抛物线y=$\frac{1}{2}$x2+nx-2与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0).
如图,抛物线y=$\frac{1}{2}$x2+nx-2与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0). 某养猪专业户利用一堵砖墙(长度足够)围成一个长方形猪栏,围猪栏的栅栏一共长40m,设这个长方形的相邻两边的长分别为x(m)和y(m).
某养猪专业户利用一堵砖墙(长度足够)围成一个长方形猪栏,围猪栏的栅栏一共长40m,设这个长方形的相邻两边的长分别为x(m)和y(m).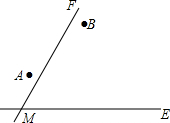 两城镇A、B与两条公路ME、MF位置如图所示,现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路ME、MF的距离也必须相等,且在∠FME的内部,那么点C应选在何处?请在图中,用尺规作图找出符合条件的点C.(不写已知、求作、作法,只保留作图痕迹)
两城镇A、B与两条公路ME、MF位置如图所示,现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路ME、MF的距离也必须相等,且在∠FME的内部,那么点C应选在何处?请在图中,用尺规作图找出符合条件的点C.(不写已知、求作、作法,只保留作图痕迹)