题目内容
3．已知函数f（x）=x2+|x-a|+1（x∈R），a是实数，求f（x）的最小值．分析 将函数化成f（x）=$\left\{\begin{array}{l}{（x+\frac{1}{2}）^{2}+\frac{3}{4}-a（x≥a）}\\{（x-\frac{1}{2}）^{2}+\frac{3}{4}+a（x＜a）}\end{array}\right.$，分类讨论即可．
解答 解：f（x）=$\left\{\begin{array}{l}{（x+\frac{1}{2}）^{2}+\frac{3}{4}-a（x≥a）}\\{（x-\frac{1}{2}）^{2}+\frac{3}{4}+a（x＜a）}\end{array}\right.$，
①当a≥$\frac{1}{2}$时，f（x）min=$\frac{3}{4}$+a；
②-$\frac{1}{2}$＜a＜$\frac{1}{2}$时，f（x）min=a2+1；
③当a≤-$\frac{1}{2}$时，f（x）min=$\frac{3}{4}$-a；
综上，f（x）的最小值=$\left\{\begin{array}{l}{\frac{3}{4}+a（a≥\frac{1}{2}）}\\{{a}^{2}+1（-\frac{1}{2}＜a＜\frac{1}{2}）}\\{\frac{3}{4}-a（a≤-\frac{1}{2}）}\end{array}\right.$．
点评 本题考查了二次函数的最小值，分类讨论思想的运用是解题的关键．
练习册系列答案
相关题目
19．
如图，AM为∠BAC的平分线，下列等式错误的是（ ）
如图，AM为∠BAC的平分线，下列等式错误的是（ ）| A． | $\frac{1}{2}$∠BAC=∠BAM | B． | ∠BAM=∠CAM | C． | ∠BAM=2∠CAM | D． | 2∠CAM=∠BAC |
如图，折叠矩形ABCD的一边AD，使点D落在BC边的点F处，已知折痕AE=5$\sqrt{5}$cm，且tan∠EFC=0.75，则矩形ABCD的周长为36cm．
8．
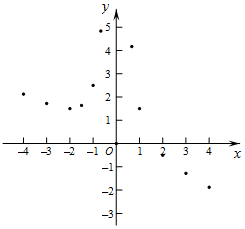有这样一个问题：探究函数y=$\frac{2}{{x}^{2}}$-$\frac{1}{2}$x的图象与性质．
小东根据学习函数的经验，对函数y=$\frac{2}{{x}^{2}}$-$\frac{1}{2}$x的图象与性质进行了探究．
下面是小东的探究过程，请补充完整，并解决相关问题：
（1）函数y=$\frac{2}{{x}^{2}}$-$\frac{1}{2}$x的自变量x的取值范围是x≠0；
（2）下表是y与x的几组对应值，求m的值；
（3）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；
（4）进一步探究发现，该函数图象在第二象限内的最低点的坐标是（-2，$\frac{3}{2}$），结合函数的图象，写出该函数的其它性质（一条即可）当x＞0时，y随x的增大而减小．
（5）根据函数图象估算方程$\frac{2}{{x}^{2}}$-$\frac{1}{2}$x=2的根为x1=-3.8，x2=-1.8．（精确到0.1）
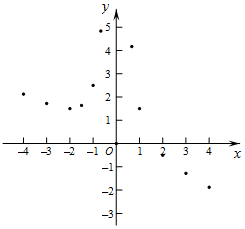有这样一个问题：探究函数y=$\frac{2}{{x}^{2}}$-$\frac{1}{2}$x的图象与性质．小东根据学习函数的经验，对函数y=$\frac{2}{{x}^{2}}$-$\frac{1}{2}$x的图象与性质进行了探究．
下面是小东的探究过程，请补充完整，并解决相关问题：
（1）函数y=$\frac{2}{{x}^{2}}$-$\frac{1}{2}$x的自变量x的取值范围是x≠0；
（2）下表是y与x的几组对应值，求m的值；
| x | … | -4 | -3 | -2 | -$\frac{3}{2}$ | -1 | -$\frac{2}{3}$ | $\frac{2}{3}$ | 1 | 2 | 3 | 4 | … |
| y | … | $\frac{17}{8}$ | $\frac{31}{18}$ | $\frac{3}{2}$ | $\frac{59}{36}$ | $\frac{5}{2}$ | $\frac{29}{6}$ | $\frac{25}{6}$ | $\frac{3}{2}$ | -$\frac{1}{2}$ | -$\frac{23}{18}$ | m | … |
（4）进一步探究发现，该函数图象在第二象限内的最低点的坐标是（-2，$\frac{3}{2}$），结合函数的图象，写出该函数的其它性质（一条即可）当x＞0时，y随x的增大而减小．
（5）根据函数图象估算方程$\frac{2}{{x}^{2}}$-$\frac{1}{2}$x=2的根为x1=-3.8，x2=-1.8．（精确到0.1）
如图是由5个全等的正方形拼成的图形，把它剪成一个大正方形，并使剪痕的条数最少．