题目内容
12．不等式组$\left\{\begin{array}{l}{x-3≥0}\\{3x＜2x+4}\end{array}\right.$的解为3≤x＜4．分析 分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集．
解答 解：解不等式x-3≥0，得：x≥3，
解不等式3x＜2x+4，得：x＜4，
∴不等式组的解集为3≤x＜4，
故答案为：3≤x＜4．
点评 本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
练习册系列答案
超能学典应用题题卡系列答案
相关题目
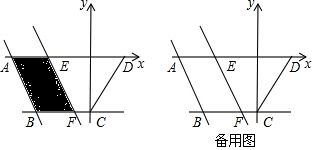
7．
如图示，若△ABC内一点P满足∠PAC=∠PBA=∠PCB，则点P为△ABC的布洛卡点．三角形的布洛卡点（Brocard point）是法国数学家和数学教育家克洛尔（A．L．Crelle 1780-1855）于1816年首次发现，但他的发现并未被当时的人们所注意，1875年，布洛卡点被一个数学爱好者法国军官布洛卡（Brocard 1845-1922）重新发现，并用他的名字命名．问题：已知在等腰直角三角形DEF中，∠EDF=90°，若点Q为△DEF的布洛卡点，DQ=1，则EQ+FQ=（ ）
如图示，若△ABC内一点P满足∠PAC=∠PBA=∠PCB，则点P为△ABC的布洛卡点．三角形的布洛卡点（Brocard point）是法国数学家和数学教育家克洛尔（A．L．Crelle 1780-1855）于1816年首次发现，但他的发现并未被当时的人们所注意，1875年，布洛卡点被一个数学爱好者法国军官布洛卡（Brocard 1845-1922）重新发现，并用他的名字命名．问题：已知在等腰直角三角形DEF中，∠EDF=90°，若点Q为△DEF的布洛卡点，DQ=1，则EQ+FQ=（ ）| A． | 5 | B． | 4 | C． | $3+\sqrt{2}$ | D． | $2+\sqrt{2}$ |
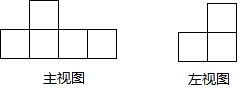如图是由大小相同的小正方体搭成的几何体的主视图和左视图，搭成这样的几何体最多需要a个这样的小正方体，则a=（ ）
1．已知a、b为两个连续的整数，且a＜$\sqrt{2}$＜b，则a+b=（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |