题目内容
15．
如图是由5个全等的正方形拼成的图形，把它剪成一个大正方形，并使剪痕的条数最少．
分析 根据拼成的大正方形的边长为$\sqrt{5}$，沿相邻的两个正方形的对角线剪开，再从三个正方形的公共顶点处剪出直角，然后拼接即可．
解答 
解：如图所示：剪痕的条数最少．
点评 本题考查了图形的剪拼，关键在于根据正方形的面积求出所拼接成的正方形的边长．
练习册系列答案
阅读快车系列答案
相关题目
10．在四边形ABCD中，AC、BD相交于O点，下列条件能判断四边形ABCD是正方形的是（ ）
| A． | OA=OC，OB=OC | B． | OA=OB=OC=OD | ||
| C． | OA=OC，OB=OD，AC=BD | D． | OA=OB=OC=OD，AC⊥BD |
10．
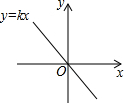已知函数y=kx的图象如图所示，则对一元二次方程x2+x+k-1=0根的情况，说法正确的是（ ）
已知函数y=kx的图象如图所示，则对一元二次方程x2+x+k-1=0根的情况，说法正确的是（ ）| A． | 没有实数根 | B． | 有两个相等的实数根 | ||
| C． | 有两个不相等的实数根 | D． | 无法确定 |
7．
如图示，若△ABC内一点P满足∠PAC=∠PBA=∠PCB，则点P为△ABC的布洛卡点．三角形的布洛卡点（Brocard point）是法国数学家和数学教育家克洛尔（A．L．Crelle 1780-1855）于1816年首次发现，但他的发现并未被当时的人们所注意，1875年，布洛卡点被一个数学爱好者法国军官布洛卡（Brocard 1845-1922）重新发现，并用他的名字命名．问题：已知在等腰直角三角形DEF中，∠EDF=90°，若点Q为△DEF的布洛卡点，DQ=1，则EQ+FQ=（ ）
如图示，若△ABC内一点P满足∠PAC=∠PBA=∠PCB，则点P为△ABC的布洛卡点．三角形的布洛卡点（Brocard point）是法国数学家和数学教育家克洛尔（A．L．Crelle 1780-1855）于1816年首次发现，但他的发现并未被当时的人们所注意，1875年，布洛卡点被一个数学爱好者法国军官布洛卡（Brocard 1845-1922）重新发现，并用他的名字命名．问题：已知在等腰直角三角形DEF中，∠EDF=90°，若点Q为△DEF的布洛卡点，DQ=1，则EQ+FQ=（ ）| A． | 5 | B． | 4 | C． | $3+\sqrt{2}$ | D． | $2+\sqrt{2}$ |
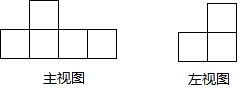如图是由大小相同的小正方体搭成的几何体的主视图和左视图，搭成这样的几何体最多需要a个这样的小正方体，则a=（ ）
5．下列各数中，是无理数的是（ ）
| A． | $\frac{22}{7}$ | B． | $\frac{π}{2}$ | C． | 2 | D． | sin30° |