题目内容
16.计算:$\frac{\sqrt{{2}^{2}-1}}{2-1}$=$\sqrt{3}$,$\frac{\sqrt{{3}^{2}-1}}{3-1}$=$\sqrt{2}$,
$\frac{\sqrt{{4}^{2}-1}}{4-1}$=$\frac{\sqrt{15}}{3}$,
$\frac{\sqrt{{5}^{2}-1}}{5-1}$=$\frac{\sqrt{6}}{2}$,…,
观察以上计算结果的变化规律,由此判断P=$\frac{\sqrt{{n}^{2}-1}}{n-1}$与Q=$\frac{\sqrt{(n+1)^{2}-1}}{(n+1)-1}$的大小关系是>.(n为大于1的整数)
分析 先化简各二次根式,然后找出其中的规律,最后依据规律找出其中的答案即可.
解答 解:$\frac{\sqrt{{2}^{2}-1}}{2-1}$=$\sqrt{3}$,
$\frac{\sqrt{{3}^{2}-1}}{3-1}$=$\frac{\sqrt{9-1}}{2}$=$\frac{\sqrt{8}}{2}$=$\sqrt{2}$,
$\frac{\sqrt{{4}^{2}-1}}{4-1}$=$\frac{\sqrt{15}}{3}$,
$\frac{\sqrt{{5}^{2}-1}}{5-1}$=$\frac{\sqrt{24}}{4}$=$\frac{\sqrt{6}}{2}$,
P=$\sqrt{\frac{{n}^{2}-1}{(n-1)^{2}}}$=$\sqrt{\frac{n+1}{n-1}}$,Q=$\sqrt{\frac{(n+1)^{2}-1}{{n}^{2}}}$=$\sqrt{\frac{n+2}{n}}$.
$\frac{n+1}{n-1}-\frac{n+2}{n}$=$\frac{{n}^{2}+n-({n}^{2}+n-2)}{n(n-1)}$=$\frac{2}{n(n-1)}$>0,
则$\frac{n+1}{n-1}>\frac{n+2}{n}$.
则$\sqrt{\frac{n+1}{n-1}}$>$\sqrt{\frac{n+2}{n}}$,即P>Q.
故答案为;$\sqrt{\sqrt{3}}$;$\sqrt{2}$;$\frac{\sqrt{15}}{3}$;$\frac{\sqrt{6}}{2}$;>.
点评 本题主要考查的是二次根式的化简与计算,比较出$\sqrt{\frac{n+1}{n-1}}$与$\sqrt{\frac{n+2}{n}}$的大小是解题的关键.

 如图,比较AB+BC与AC的大小关系是AB+BC>AC,它的根据是两点之间线段最短.
如图,比较AB+BC与AC的大小关系是AB+BC>AC,它的根据是两点之间线段最短.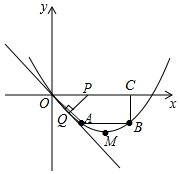 已知,如图,在四边形OABC中,AB∥OC,BC⊥x轴于点C,A(1,-1),B(3,-1),动点P从点O出发,沿着x轴正方向以每秒2个单位长度的速度移动,过点P作PQ垂直于直线OA,垂足为点Q,设点P移动的时间t秒(0<t<2),△OPQ与四边形OABC重叠部分的面积为S.
已知,如图,在四边形OABC中,AB∥OC,BC⊥x轴于点C,A(1,-1),B(3,-1),动点P从点O出发,沿着x轴正方向以每秒2个单位长度的速度移动,过点P作PQ垂直于直线OA,垂足为点Q,设点P移动的时间t秒(0<t<2),△OPQ与四边形OABC重叠部分的面积为S.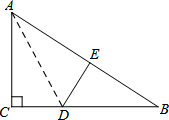 如图,折叠Rt△ABC,使直角边AC落在斜边AB上,点C落到点E处,已知AC=6cm,BC=8cm,则CD的长为( )
如图,折叠Rt△ABC,使直角边AC落在斜边AB上,点C落到点E处,已知AC=6cm,BC=8cm,则CD的长为( )