题目内容
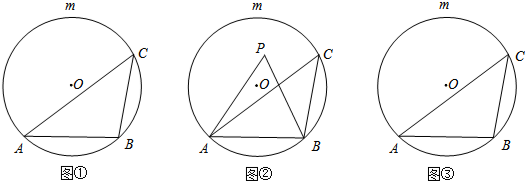
4.如图①,AB是⊙O的一条弦,点C是优弧$\widehat{AmB}$上一点.(1)若∠ACB=45°,点P是⊙O上一点(不与A、B重合),则∠APB=45°或135°;
(2)如图②,若点P是弦AB与$\widehat{AmB}$所围成的弓形区域(不含弦AB与$\widehat{AmB}$)内一点.求证:∠APB>∠ACB;
(3)请在图③中直接用阴影部分表示出在弦AB与$\widehat{AmB}$所围成的弓形区域内满足∠ACB<∠APB<2∠ACB的点P所在的范围.
分析 (1)根据题意可知,存在两种情况,针对两种情况,可以画出相应的图形,由题目中的信息和同弧所对的圆周角相等,圆内接四边形对角互补,可以分别求得两种情况下∠APB的度数,本题得以解决;
(2)根据题意画出相应的图形,根据三角形的外角大于任何一个和它不相邻的内角,可以证明结论成立,本题得以解决;
(3)根据题意和第(2)问,可以画出满足∠ACB<∠APB<2∠ACB的点P所在的范围,本题得以解决.
解答  (1)解:如右图①所示,
(1)解:如右图①所示,
根据题意可分两种情况,
第一种情况,当点P在P1时,
可知,∠AP1B=∠ACB=45°;
第二种情况,当点P在P2时,
∵四边形ACBP2是圆内接四边形,
∴∠AP2B+∠ACB=180°,
∵∠ACB=45°,
∴∠AP2B=135°,
故答案为:45°或135°;
(2)证明:如下图②所示,延长AP交⊙O于点Q,连接BQ.
则∠PQB=∠ACB,
∵∠APB为△PQB的一个外角,
∴∠APB>∠PQB,
即∠APB>∠ACB;
(3)点P所在的范围如下图③所示,
点评 本题考查圆的综合题、同弧所对的圆周角的关系、圆内接四边形对角的关系、三角形的外角和内角的关系,解题的关键是明确题意,画出相应的图形,找出所求问题需要的条件,利用分类讨论的数学思想解答问题.

练习册系列答案
相关题目
14.单项式-$\frac{{a}^{2}b}{7}$的系数和次数分别是( )
| A. | -7,2 | B. | -$\frac{1}{7}$,2 | C. | -$\frac{1}{7}$,3 | D. | $\frac{1}{7}$,3 |
9.下列图形选自历届世博会会徽,其中是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
14.方程组$\left\{\begin{array}{l}{2x+y=3}\\{3x-z=7}\\{x-y+3z=0}\end{array}\right.$的解为( )
| A. | $\left\{\begin{array}{l}{x=2}\\{y=1}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=2}\\{y=-1}\\{z=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=-1}\\{z=-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2}\\{y=1}\\{z=1}\end{array}\right.$ |
 在学习“用直尺和圆规作射线OC,使它平分∠AOB”时,教科书介绍如下:*作法:(1)以O为圆心,任意长为半径作弧,交OA于D,交OB于E;
在学习“用直尺和圆规作射线OC,使它平分∠AOB”时,教科书介绍如下:*作法:(1)以O为圆心,任意长为半径作弧,交OA于D,交OB于E;