题目内容
9.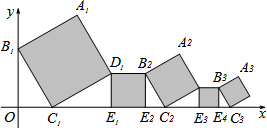 已知在平面直角坐标系中放置了5个如图所示的正方形(用阴影表示),点B1在y轴上,点C1,E1,E2,C2,E3,E4,C3在x轴上.若正方形A1B1C1D1的边长为2,∠B1C1O=60°,B1C1∥B2C2∥B3C3,则点A3到x轴的距离是( )
已知在平面直角坐标系中放置了5个如图所示的正方形(用阴影表示),点B1在y轴上,点C1,E1,E2,C2,E3,E4,C3在x轴上.若正方形A1B1C1D1的边长为2,∠B1C1O=60°,B1C1∥B2C2∥B3C3,则点A3到x轴的距离是( )| A. | $\frac{1+\sqrt{3}}{9}$ | B. | $\frac{3+\sqrt{3}}{9}$ | C. | $\frac{3+\sqrt{3}}{3}$ | D. | $\frac{1+\sqrt{3}}{3}$ |
分析 根据两直线平行,同位角相等可得∠B3C3O=∠B2C2O=∠B1C1O=60°,然后解直角三角形求出OC1、C1E、E1E2、E2C2、C2E3、E3E4、E4C3,再求出B3C3,过点A3延长正方形的边交x轴于M,过点A3作A3N⊥x轴于N,先求出A3M,再解直角三角形求出A3N,得出点A3到x轴的距离.
解答 解:∵B1C1∥B2C2∥B3C3,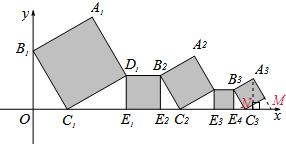
∴∠B3C3O=∠B2C2O=∠B1C1O=60°,
∵正方形A1B1C1D1的边长为1,
∴OC1=$\frac{1}{2}$×2=1,
C1E=$\frac{\sqrt{3}}{2}$×2=$\sqrt{3}$,
E1E2=$\frac{1}{2}$×2=1,
E2C2=1×$\frac{\sqrt{3}}{3}$=$\frac{\sqrt{3}}{3}$,
C2E3=E2B2=1,
E3E4=E2C2=$\frac{\sqrt{3}}{3}$,E4C3=$\frac{\sqrt{3}}{3}$×$\frac{\sqrt{3}}{3}$=$\frac{1}{3}$,
∴B3C3=2E4C3=$\frac{2}{3}$,
过点A3延长正方形的边交x轴于M,过点A3作A3N⊥x轴于N,如图所示:
则A3M=$\frac{2}{3}$+$\frac{2}{3}$×$\frac{\sqrt{3}}{3}$=$\frac{6+2\sqrt{3}}{9}$,
∴A3N=A3M•sin60°=$\frac{6+2\sqrt{3}}{9}$×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}+1}{3}$;
故选:D.
点评 此题主要考查了正方形的性质以及解直角三角形的知识,得出正方形各边长是解题关键.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
14.一个五次六项式加上一个六次七项式等于几次几项式( )
| A. | 十一次十三项式 | B. | 六次十三项式 | C. | 六次多项式 | D. | 六次整式 |
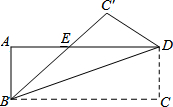 如图,长方形ABCD中,AB=4,BC=8,将长方形沿BC折叠,点C落在C′处.△BDE的面积是多少?
如图,长方形ABCD中,AB=4,BC=8,将长方形沿BC折叠,点C落在C′处.△BDE的面积是多少? 已知a、b、c三个数在数轴上对应点的位置如图所示,下列几个判断:①a<c<b;②-a<b;③a+b>0;④c-a<0中,错误的个数是( )
已知a、b、c三个数在数轴上对应点的位置如图所示,下列几个判断:①a<c<b;②-a<b;③a+b>0;④c-a<0中,错误的个数是( )