题目内容
19.如图,△ABC中,AB=AC,BAC=90,BC=6cm,直线CM⊥BC,在射线CB上取点D,在直线CM上取点E,使CD=2CE.(1)若△ABD的面积为6cm,求CD的长;
(2)若△ABC≌△ACE,求CD的长.(可在备用图中画出具体图形)
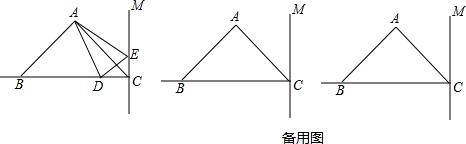
分析 (1)作AM⊥BC于M,根据等腰三角形三线合一的性质得出BM=CM,然后根据直角三角形斜边中线的性质得出AM=$\frac{1}{2}$BC=3cm,根据三角形面积求得BD,进而求得CD的长;
(2)根据△ABC≌△ACE求得CE=BC=6cm,然后根据CD=2CE即可求得CD的长.
解答 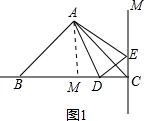 解:(1)如图1,作AM⊥BC于M,
解:(1)如图1,作AM⊥BC于M,
∵AB=AC,
∴BM=CM,
∵∠BAC=90,
∴AM=$\frac{1}{2}$BC=3cm,
∵△ABD的面积为6cm,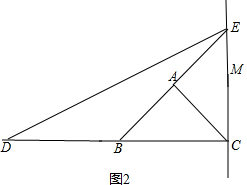
∴$\frac{1}{2}$BD•AM=6,即$\frac{1}{2}$BD•3=6,
∴BD=4,
∴CD=BC-BD=2cm;
(2)如图2,∵△ABC≌△ACE,
∴CE=BC=6cm,
∵CD=2CE,
∴CD=12cm.
点评 本题考查了等腰三角形的性质,直角三角形斜边中线的性质以及三角形全等的性质,熟练掌握这些性质是解题的关键.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
9.下列说法正确的是( )
| A. | 等弧所对的圆心角相等 | |
| B. | 三角形的外心到这个三角形的三边距离相等 | |
| C. | 经过三点可以作一个圆 | |
| D. | 相等的圆心角所对的弧相等 |
7.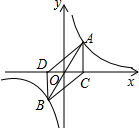 如图:A,B是函数y=$\frac{2}{x}$的图象上关于原点O点对称的任意两点,AC垂直于x轴于点C,BD垂直于y轴于点D,设四边形ADBC的面积为S,则( )
如图:A,B是函数y=$\frac{2}{x}$的图象上关于原点O点对称的任意两点,AC垂直于x轴于点C,BD垂直于y轴于点D,设四边形ADBC的面积为S,则( )
 如图:A,B是函数y=$\frac{2}{x}$的图象上关于原点O点对称的任意两点,AC垂直于x轴于点C,BD垂直于y轴于点D,设四边形ADBC的面积为S,则( )
如图:A,B是函数y=$\frac{2}{x}$的图象上关于原点O点对称的任意两点,AC垂直于x轴于点C,BD垂直于y轴于点D,设四边形ADBC的面积为S,则( )| A. | S=2 | B. | 2<S<4 | C. | S=4 | D. | S>4 |
4.
| 计算: (1)28+(-72) | (2)0+(-5) | (3)-$\frac{1}{5}$+(+$\frac{1}{6}$) |
| (4)(-3)-(-5) | (5)$({-3\frac{1}{2}})-5\frac{1}{4}$ | (6)(-8)+(-5)-(+5) |
| (7)-37-40+3-22 | (7)$(({-4})×({-\frac{3}{4}})×2$ | (8)(-5)×(-4)×3×(-2) |
| (9)-12÷$\frac{1}{4}÷({-\frac{8}{3}})$ | (10)$({\frac{1}{3}-\frac{5}{6}+\frac{7}{9}})÷({\frac{1}{18}})$ | (11)9$\frac{15}{16}×({-8})$ |
| (12)100÷$\frac{1}{8}×({-8})$ | (13)$1÷({-\frac{2}{7}})×\frac{1}{7}$ | (14)$\frac{1}{2}×({-\frac{4}{15}})÷\frac{2}{3}$. |
9.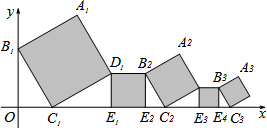 已知在平面直角坐标系中放置了5个如图所示的正方形(用阴影表示),点B1在y轴上,点C1,E1,E2,C2,E3,E4,C3在x轴上.若正方形A1B1C1D1的边长为2,∠B1C1O=60°,B1C1∥B2C2∥B3C3,则点A3到x轴的距离是( )
已知在平面直角坐标系中放置了5个如图所示的正方形(用阴影表示),点B1在y轴上,点C1,E1,E2,C2,E3,E4,C3在x轴上.若正方形A1B1C1D1的边长为2,∠B1C1O=60°,B1C1∥B2C2∥B3C3,则点A3到x轴的距离是( )
 已知在平面直角坐标系中放置了5个如图所示的正方形(用阴影表示),点B1在y轴上,点C1,E1,E2,C2,E3,E4,C3在x轴上.若正方形A1B1C1D1的边长为2,∠B1C1O=60°,B1C1∥B2C2∥B3C3,则点A3到x轴的距离是( )
已知在平面直角坐标系中放置了5个如图所示的正方形(用阴影表示),点B1在y轴上,点C1,E1,E2,C2,E3,E4,C3在x轴上.若正方形A1B1C1D1的边长为2,∠B1C1O=60°,B1C1∥B2C2∥B3C3,则点A3到x轴的距离是( )| A. | $\frac{1+\sqrt{3}}{9}$ | B. | $\frac{3+\sqrt{3}}{9}$ | C. | $\frac{3+\sqrt{3}}{3}$ | D. | $\frac{1+\sqrt{3}}{3}$ |

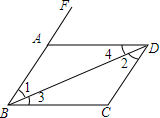 按图填空,并在横线内标明理由:
按图填空,并在横线内标明理由: