题目内容
18．已知等腰三角形的周长是14cm，底边和腰的比是3：2，求各边的长．分析 因为等腰三角形的两腰相等，底边与腰的比为3：2，所以三条边的比是3：2：2，用周长除以（3+2+2）即可求出每一份的长度，进一步求出三边的长．
解答 解：由题意得：三边之比为：3：2：2；
14÷（3+2+2）
=14÷7
=2（cm），
2×3=6（cm），
2×2=4（cm）．
答：三边长分别为6cm，4cm，4cm．
点评 考查了等腰三角形的性质，本题关键是求出周长对应的总份数；然后再根据乘法的意义解答．
练习册系列答案
相关题目
9．
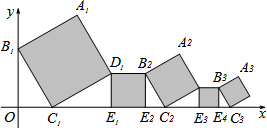已知在平面直角坐标系中放置了5个如图所示的正方形（用阴影表示），点B1在y轴上，点C1，E1，E2，C2，E3，E4，C3在x轴上．若正方形A1B1C1D1的边长为2，∠B1C1O=60°，B1C1∥B2C2∥B3C3，则点A3到x轴的距离是（ ）
已知在平面直角坐标系中放置了5个如图所示的正方形（用阴影表示），点B1在y轴上，点C1，E1，E2，C2，E3，E4，C3在x轴上．若正方形A1B1C1D1的边长为2，∠B1C1O=60°，B1C1∥B2C2∥B3C3，则点A3到x轴的距离是（ ）| A． | $\frac{1+\sqrt{3}}{9}$ | B． | $\frac{3+\sqrt{3}}{9}$ | C． | $\frac{3+\sqrt{3}}{3}$ | D． | $\frac{1+\sqrt{3}}{3}$ |
请在图中作出△ABC的角平分线BD（要求保留作图痕迹）．
10．设6-$\sqrt{3}$的整数部分为a，小数部分为b，则a-$\frac{1}{b}$的值为（ ）
| A． | 2-$\sqrt{3}$ | B． | $\sqrt{3}$ | C． | -$\sqrt{3}$ | D． | 2$+\sqrt{3}$ |
7．1-2+3-4+5-6+…+2005-2006的结果是（ ）
| A． | 0 | B． | 100 | C． | -1003 | D． | 1003 |
