题目内容
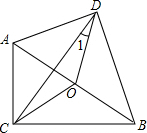 如图,在四边形ABCD中,∠ACB=∠ADB=90°,O是AB的中点,若∠CAB=60°,∠DBA=40°,则∠1=
如图,在四边形ABCD中,∠ACB=∠ADB=90°,O是AB的中点,若∠CAB=60°,∠DBA=40°,则∠1=考点:直角三角形斜边上的中线
专题:
分析:由∠ACB=∠ADB=90°,可得△ABC和△ABD都是Rt△,由O是AB的中点,根据直角三角形斜边上的中线等于斜边的一半,可得OC=OD=OA=OB,进而可得∠1=∠DCO,由∠CAB=60°,∠DBA=40°,可得∠∠AOD和∠AOC的度数,然后根据三角形的内角和定理可求∠1的度数.
解答:解:∵,∠ACB=∠ADB=90°,O是AB的中点,
∴OC=OA=OD=OB,
∵∠CAB=60°,∠DBA=40°,
∴∠AOC=60°,∠ODB=∠DBA=40°,
∴∠AOD=80°,
∴∠COD=60°+80°=140°,
∵OC=OD,
∴∠OCD=∠1,
∴∠1=
(180°-∠COD)=20°.
故答案为20.
∴OC=OA=OD=OB,
∵∠CAB=60°,∠DBA=40°,
∴∠AOC=60°,∠ODB=∠DBA=40°,
∴∠AOD=80°,
∴∠COD=60°+80°=140°,
∵OC=OD,
∴∠OCD=∠1,
∴∠1=
| 1 |
| 2 |
故答案为20.
点评:本题考查了直角三角形斜边上的中线的性质,等腰三角形的判定和性质三角形的内角和定理的应用等,熟练掌握和正确应用定理性质是解题的关键.

练习册系列答案
相关题目
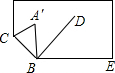 如图所示,将一长方形纸的一角斜折过去,使顶点A落在A′处,BC为折痕,如果BD为∠A′BE的平分线,则∠CBD=( )
如图所示,将一长方形纸的一角斜折过去,使顶点A落在A′处,BC为折痕,如果BD为∠A′BE的平分线,则∠CBD=( )| A、90° | B、80° |
| C、100° | D、70° |
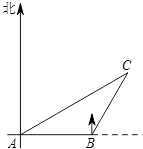 如图,一艘渔船正自西向东航行追赶鱼群,在A处望见岛C在船的北偏东60°方向,前进20海里到达B处,此时望见岛C在船的北偏东30°方向,以岛C为中心的12海里内为军事演习的危险区.请通过计算说明:如果这艘渔船继续向东追赶鱼群是否有进入危险区的可能.(参考数据:
如图,一艘渔船正自西向东航行追赶鱼群,在A处望见岛C在船的北偏东60°方向,前进20海里到达B处,此时望见岛C在船的北偏东30°方向,以岛C为中心的12海里内为军事演习的危险区.请通过计算说明:如果这艘渔船继续向东追赶鱼群是否有进入危险区的可能.(参考数据: 已知二次函数y=-x2+(m-1)x+m.
已知二次函数y=-x2+(m-1)x+m.