题目内容
 如图,已知函数y=x+1的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0,-1),与x轴以及y=x+1的图象分别交于点C、D,且点D的坐标为(1,n),
如图,已知函数y=x+1的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0,-1),与x轴以及y=x+1的图象分别交于点C、D,且点D的坐标为(1,n),(1)点A的坐标是
(2)x取何值时,函数y=kx+b的函数值大于函数y=x+1的函数值;
(3)求四边形AOCD的面积;
(4)是否存在y轴上的点P,使得以点P,B,D为顶点的三角形是等腰三角形?若存在求出点P的坐标;若不存在,请说明理由.
考点:一次函数综合题
专题:
分析:(1)由函数y=x+1的图象与y轴交于点A,可求点A的坐标,由y=x+1的图象过点D,且点D的坐标为(1,n),可得D的坐标,由一次函数y=kx+b的图象经过点B(0,-1)与D(1,2),即可求出k,b的值.
(2)根据图象即可得出答案;
(3)先求出点D的坐标,再求出BD的解析式,然后根据S四边形AOCD=S△AOD+S△COD即可求解;
(4)分三种情况讨论:①当DP=DB时,②当BP=DB时,③当PB=PD时分别求解.
(2)根据图象即可得出答案;
(3)先求出点D的坐标,再求出BD的解析式,然后根据S四边形AOCD=S△AOD+S△COD即可求解;
(4)分三种情况讨论:①当DP=DB时,②当BP=DB时,③当PB=PD时分别求解.
解答:解:(1)∵函数y=x+1的图象与y轴交于点A,
∴令x=0时,y=0+1,解得y=1,
∴A(0,1),
∵y=x+1的图象过点D,且点D的坐标为(1,n),
∴n=1+1=2,
∴D(1,2),
∵一次函数y=kx+b的图象经过点B(0,-1)与D(1,2),
∴
解得
,
∴一次函数的表达式为y=3x-1
故答案为:(0,1),2,3,-1.
(2)由一次函数图象可得当x>1时,函数y=kx+b的函数值大于函数y=x+1的函数值;
(3)∵D(1,2),
∴直线BD的解析式为y=3x-1,
∴A(0,1),C(
,0)
∴S四边形AOCD=S△AOD+S△COD=
×1×1+
×
×2=
(4)①当DP=DB时,设P(0,y),
∵B(0,-1),D(1,2),
∴DP2=12+(y-2)2=DB2=12+(2+1)2,
∴P(0,5);
②当BP=DB时,DB=
,∴P(0,-1-
)或P(0,
-1);
③当PB=PD时,设P(0,a),则(a+1)2=1+(2-a)2,解得a=
,
∴P(0,
).
综上所述点P的坐标为(0,5),(0,-1-
),P(0,
-1)或(0,
).
∴令x=0时,y=0+1,解得y=1,
∴A(0,1),
∵y=x+1的图象过点D,且点D的坐标为(1,n),
∴n=1+1=2,
∴D(1,2),
∵一次函数y=kx+b的图象经过点B(0,-1)与D(1,2),
∴
|
|
∴一次函数的表达式为y=3x-1
故答案为:(0,1),2,3,-1.
(2)由一次函数图象可得当x>1时,函数y=kx+b的函数值大于函数y=x+1的函数值;
(3)∵D(1,2),
∴直线BD的解析式为y=3x-1,
∴A(0,1),C(
| 1 |
| 3 |
∴S四边形AOCD=S△AOD+S△COD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 5 |
| 6 |
(4)①当DP=DB时,设P(0,y),
∵B(0,-1),D(1,2),
∴DP2=12+(y-2)2=DB2=12+(2+1)2,
∴P(0,5);
②当BP=DB时,DB=
| 10 |
| 10 |
| 10 |
③当PB=PD时,设P(0,a),则(a+1)2=1+(2-a)2,解得a=
| 2 |
| 3 |
∴P(0,
| 2 |
| 3 |
综上所述点P的坐标为(0,5),(0,-1-
| 10 |
| 10 |
| 2 |
| 3 |
点评:本题考查了一次函数综合知识,难度适中,解题的关键是掌握分类讨论思想的运用.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 二次函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c=0的根的情况是( )
二次函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c=0的根的情况是( )| A、有两个不相等的实数根 |
| B、有两个异号实数根 |
| C、有两个相等的实数根 |
| D、无实数根 |
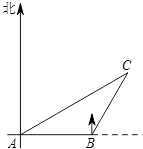 如图,一艘渔船正自西向东航行追赶鱼群,在A处望见岛C在船的北偏东60°方向,前进20海里到达B处,此时望见岛C在船的北偏东30°方向,以岛C为中心的12海里内为军事演习的危险区.请通过计算说明:如果这艘渔船继续向东追赶鱼群是否有进入危险区的可能.(参考数据:
如图,一艘渔船正自西向东航行追赶鱼群,在A处望见岛C在船的北偏东60°方向,前进20海里到达B处,此时望见岛C在船的北偏东30°方向,以岛C为中心的12海里内为军事演习的危险区.请通过计算说明:如果这艘渔船继续向东追赶鱼群是否有进入危险区的可能.(参考数据:
