题目内容
11.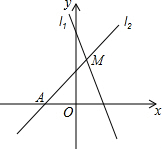 如图,已知直线l1:y=-2x+4与直线l2:y=kx+b(k≠0)在第一象限交于点M.若直线l2与x轴的交点为A(-2,0),则k的取值范围是( )
如图,已知直线l1:y=-2x+4与直线l2:y=kx+b(k≠0)在第一象限交于点M.若直线l2与x轴的交点为A(-2,0),则k的取值范围是( )| A. | -2<k<2 | B. | -2<k<0 | C. | 0<k<4 | D. | 0<k<2 |
分析 首先根据直线l2与x轴的交点为A(-2,0),求出k、b的关系;然后求出直线l1、直线l2的交点坐标,根据直线l1、直线l2的交点横坐标、纵坐标都大于0,求出k的取值范围即可.
解答 解:∵直线l2与x轴的交点为A(-2,0),
∴-2k+b=0,
∴$\left\{\begin{array}{l}{y=-2x+4}\\{y=kx+2k}\end{array}\right.$
解得$\left\{\begin{array}{l}{x=\frac{4-2k}{k+2}}\\{y=\frac{8k}{k+2}}\end{array}\right.$
∵直线l1:y=-2x+4与直线l2:y=kx+b(k≠0)的交点在第一象限,
∴$\left\{\begin{array}{l}{\frac{4-2k}{k+2}>0}\\{\frac{8k}{k+2}>0}\end{array}\right.$
解得0<k<2.
故选:D.
点评 此题主要考查了两条直线的相交问题,以及一次函数图象的点的特征,要熟练掌握.

练习册系列答案
相关题目
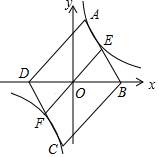 如图,点B,D分别在x轴的正、负半轴上,OB=OD,以BD为对角线作?ABCD,使点A、C分别落在反比例函数y=$\frac{k}{x}$的第一、三象限的图象上,且S?ABCD=28.AB、CD分别交反比例图象于点E、F,连结EF.当四边形BEFC是平行四边形时,k的值是$\frac{14}{3}$.
如图,点B,D分别在x轴的正、负半轴上,OB=OD,以BD为对角线作?ABCD,使点A、C分别落在反比例函数y=$\frac{k}{x}$的第一、三象限的图象上,且S?ABCD=28.AB、CD分别交反比例图象于点E、F,连结EF.当四边形BEFC是平行四边形时,k的值是$\frac{14}{3}$.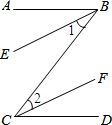 (1)完成下面的推理说明:
(1)完成下面的推理说明: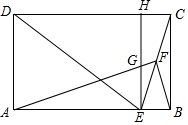 如图,在矩形ABCD中,E为AB边上一点,EC平分∠DEB,F为CE的中点,连接AF,BF,过点E作EH∥BC分别交AF,CD于G,H两点.
如图,在矩形ABCD中,E为AB边上一点,EC平分∠DEB,F为CE的中点,连接AF,BF,过点E作EH∥BC分别交AF,CD于G,H两点.
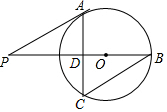 如图,已知⊙O的半径为5,PA是⊙O的一条切线,切点为A,连接PO并延长,交⊙O于点B,过点A作AC⊥PB交⊙O于点C、交PB于点D,连接BC,当∠P=30°时,
如图,已知⊙O的半径为5,PA是⊙O的一条切线,切点为A,连接PO并延长,交⊙O于点B,过点A作AC⊥PB交⊙O于点C、交PB于点D,连接BC,当∠P=30°时,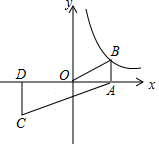 已知反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D.
已知反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D. 如图,正方形ABCD中内接正三角形AEF.求证:S△EFC=S△ABE+S△ADF.
如图,正方形ABCD中内接正三角形AEF.求证:S△EFC=S△ABE+S△ADF.