题目内容
16.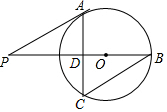 如图,已知⊙O的半径为5,PA是⊙O的一条切线,切点为A,连接PO并延长,交⊙O于点B,过点A作AC⊥PB交⊙O于点C、交PB于点D,连接BC,当∠P=30°时,
如图,已知⊙O的半径为5,PA是⊙O的一条切线,切点为A,连接PO并延长,交⊙O于点B,过点A作AC⊥PB交⊙O于点C、交PB于点D,连接BC,当∠P=30°时,(1)求弦AC的长;
(2)求证:BC∥PA.
分析 (1)连接OA,由于PA是⊙O的切线,从而可求出∠AOD=60°,由垂径定理可知:AD=DC,由锐角三角函数即可求出AC的长度.
(2)由于∠AOP=60°,所以∠BOA=120°,从而由圆周角定理即可求出∠BCA=60°,从而可证明BC∥PA
解答 解:(1)连接OA,
∵PA是⊙O的切线,
∴∠PAO=90°
∵∠P=30°,
∴∠AOD=60°,
∵AC⊥PB,PB过圆心O,
∴AD=DC
在Rt△ODA中,AD=OA•sin60°=$\frac{5\sqrt{3}}{2}$
∴AC=2AD=5$\sqrt{3}$
(2)∵AC⊥PB,∠P=30°,
∴∠PAC=60°,
∵∠AOP=60°
∴∠BOA=120°,
∴∠BCA=60°,
∴∠PAC=∠BCA
∴BC∥PA
点评 本题考查圆的综合问题,涉及切线的性质,解直角三角形,平行线的判定等知识,综合程度较高,属于中等题型.

练习册系列答案
相关题目
7.下列命题中,是真命题的是( )
| A. | 两条直线被第三条直线所截,同位角相等 | |
| B. | 相等的角是对顶角 | |
| C. | 同旁内角互补,两直线平行 | |
| D. | 互补的两个角一定有一个锐角,一个钝角 |
11.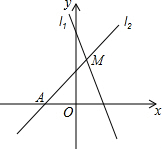 如图,已知直线l1:y=-2x+4与直线l2:y=kx+b(k≠0)在第一象限交于点M.若直线l2与x轴的交点为A(-2,0),则k的取值范围是( )
如图,已知直线l1:y=-2x+4与直线l2:y=kx+b(k≠0)在第一象限交于点M.若直线l2与x轴的交点为A(-2,0),则k的取值范围是( )
 如图,已知直线l1:y=-2x+4与直线l2:y=kx+b(k≠0)在第一象限交于点M.若直线l2与x轴的交点为A(-2,0),则k的取值范围是( )
如图,已知直线l1:y=-2x+4与直线l2:y=kx+b(k≠0)在第一象限交于点M.若直线l2与x轴的交点为A(-2,0),则k的取值范围是( )| A. | -2<k<2 | B. | -2<k<0 | C. | 0<k<4 | D. | 0<k<2 |
1.以坐标原点O为圆心,作半径为2的圆,若直线y=-x+b与⊙O相交,则b的取值范围是( )
| A. | 0≤b<2$\sqrt{2}$ | B. | -2$\sqrt{2}≤b≤2\sqrt{2}$ | C. | -2$\sqrt{3}<b<$2$\sqrt{3}$ | D. | -2$\sqrt{2}$<b<2$\sqrt{2}$ |
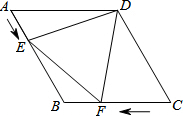 如图,在菱形ABCD中,AB=6cm,∠A=60°,点E以1cm/s的速度沿AB边由A向B匀速运动,同时点F以2cm/s的速度沿CB边由C向B运动,F到达点B时两点同时停止运动.设运动时间为t秒,当△DEF为等边三角形时,t的值为( )
如图,在菱形ABCD中,AB=6cm,∠A=60°,点E以1cm/s的速度沿AB边由A向B匀速运动,同时点F以2cm/s的速度沿CB边由C向B运动,F到达点B时两点同时停止运动.设运动时间为t秒,当△DEF为等边三角形时,t的值为( )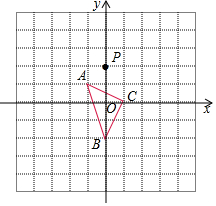 如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-1,1),B(0,-2),C(1,0),点P(0,2)绕点A旋转180°得到点P1,点P1绕点B旋转180°得到点P2,点P2绕点C旋转180°得到点P3,点P3绕点A旋转180°得到点P4,…,按此作法进行下去,则点P2017的坐标为(-2,0).
如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-1,1),B(0,-2),C(1,0),点P(0,2)绕点A旋转180°得到点P1,点P1绕点B旋转180°得到点P2,点P2绕点C旋转180°得到点P3,点P3绕点A旋转180°得到点P4,…,按此作法进行下去,则点P2017的坐标为(-2,0).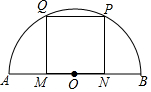 如图,点M,N在半圆的直径AB上,点P,Q在$\widehat{AB}$上,四边形MNPQ为正方形.若半圆的半径为$\sqrt{5}$,则正方形的边长为2.
如图,点M,N在半圆的直径AB上,点P,Q在$\widehat{AB}$上,四边形MNPQ为正方形.若半圆的半径为$\sqrt{5}$,则正方形的边长为2. 定义:有三个内角相等的四边形叫三等角四边形.
定义:有三个内角相等的四边形叫三等角四边形.