题目内容
3．下列各分式中，最简分式是（ ）| A． | $\frac{x}{{x}^{2}+1}$ | B． | $\frac{{m}^{2}-{n}^{2}}{m+n}$ | C． | $\frac{a+b}{{a}^{2}-{b}^{2}}$ | D． | $\frac{x+y}{{x}^{2}y+x{y}^{2}}$ |
分析 最简分式的标准是分子，分母中不含有公因式，不能再约分．判断的方法是把分子、分母分解因式，并且观察有无互为相反数的因式，这样的因式可以通过符号变化化为相同的因式从而进行约分
解答 解：A、$\frac{x}{{x}^{2}+1}$的分子、分母都不能再分解，且不能约分，是最简分式；
B、$\frac{{m}^{2}-{n}^{2}}{m+n}$=m-n；
C、$\frac{a+b}{{a}^{2}-{b}^{2}}$=$\frac{1}{a-b}$；
D、$\frac{x+y}{{x}^{2}y+x{y}^{2}}$=$\frac{1}{x+y}$；
故选A．
点评 本题考查了最简分式，分式的化简过程，首先要把分子分母分解因式，互为相反数的因式是比较易忽视的问题．在解题中一定要引起注意．
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
13．方程2x2=x的根为（ ）
| A． | x=$\frac{1}{2}$ | B． | x=0 | C． | x1=2，x2=0 | D． | x=$\frac{1}{2}$或x=0 |
14．若向量$\overrightarrow{a}$与$\overrightarrow{b}$均为单位向量，则下列结论中正确的是（ ）
| A． | $\overrightarrow{a}$=$\overrightarrow{b}$ | B． | $\overrightarrow{a}$=-$\overrightarrow{b}$ | C． | |$\overrightarrow{a}$|=|$\overrightarrow{b}$| | D． | $\overrightarrow{a}$=1 |
8．一元二次方程x2=2的解是（ ）
| A． | x=2或x=-2 | B． | x=2 | C． | x=4或x=-4 | D． | x=$\sqrt{2}$或x=-$\sqrt{2}$ |
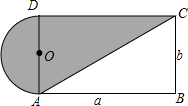设计一个商标图案（如图阴影部分），其中O为半圆的圆心，AB=a，BC=b，