题目内容
6．函数y=$\frac{1-k}{x}$的图象与直线y=-x没有交点，那么k的取值范围是（ ）| A． | k＞1 | B． | k＜1 | C． | k＞-1 | D． | k＜-1 |
分析 函数y=$\frac{1-k}{x}$的图象与直线y=-x没有交点，根据正比例函数及反比例函数的性质作答即可．
解答 解：直线y=-x中过第二、四象限，
要使两个函数没交点，
那么函数y=$\frac{1-k}{x}$的图象必须位于第一、三象限，
那么1-k＞0，
即k＜1．
故选：B．
点评 本题考查了反比例函数与一次函数的交点问题，解题的关键是根据一次函数和反比例函数的性质、结合函数图象解答．
练习册系列答案
相关题目
如图，EF⊥BC，DE⊥AB，∠B=∠ADE=30°．
17．
如图，⊙O的直径AB=8，P为⊙O上任一点（不同于A、B两点），∠APB的平分线交⊙O于点C，弦EF经过AC、BC的中点M、N，则弦EF的长为（ ）
如图，⊙O的直径AB=8，P为⊙O上任一点（不同于A、B两点），∠APB的平分线交⊙O于点C，弦EF经过AC、BC的中点M、N，则弦EF的长为（ ）| A． | 2$\sqrt{5}$ | B． | 2$\sqrt{3}$ | C． | 3$\sqrt{3}$ | D． | 4$\sqrt{3}$ |
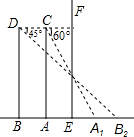如图所示，细心的王聪站立在镜子EF前的A处时，此时他看自己的脚在镜中的像A1的俯角为60°；如果王聪向后退0.3米到B处，这时他看自己的脚在镜中的像B1的俯角为45°．求王聪的眼睛到地面的距离BD．（结果精确到0.01米，参考数据：$\sqrt{3}≈1.73$）
18．买1根油条和3个大饼共7元，买3根油条和1个大饼共5元．下列说法中正确的是（ ）
| A． | 买1根油条和1个大饼共2.5元 | B． | 2根油条比1个大饼便宜 | ||
| C． | 买2根油条和4个大饼共9元 | D． | 买5根油条和7个大饼共19元 |