题目内容
11.(1)计算:$\frac{{x}^{2}+2x-4}{x-2}$+$\frac{{x}^{2}}{2-x}$(2)先化简,再求值:$\frac{a-2}{{a}^{2}-1}$÷(a-1-$\frac{2a-1}{a+1}$),其中a=$\frac{1}{2}$.
分析 (1)首先对分式进行通分,然后利用同分母的减法法则求解;
(2)首先对括号内的分式进行通分相加,把除法转化为乘法,计算乘法即可化简,然后代入a的值求解.
解答 解:(1)原式=$\frac{{x}^{2}+2x-4-{x}^{2}}{x-2}$
=$\frac{2x-4}{x-2}$
=2;
(2)原式=$\frac{a-2}{{a}^{2}-1}$÷$\frac{(a+1)(a-1)-(2a-1)}{a+1}$
=$\frac{a-2}{{a}^{2}-1}$÷$\frac{{a}^{2}-1-2a+1}{a+1}$
=$\frac{a-2}{(a+1)(a-1)}$•$\frac{a+1}{a(a-2)}$
=$\frac{1}{a(a-1)}$
=$\frac{1}{{a}^{2}-a}$.
当a=$\frac{1}{2}$时,原式=-4.
点评 本题考查了分式的化简求值,正确进行通分、约分是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
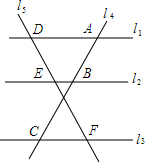 如图,两条直线被三条平行线所截,且$\frac{DE}{EF}$=$\frac{2}{3}$,AB=6,求AC的长.
如图,两条直线被三条平行线所截,且$\frac{DE}{EF}$=$\frac{2}{3}$,AB=6,求AC的长.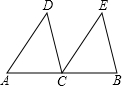 已知,如图,AC=BC,CD∥BE,且CD=BE.
已知,如图,AC=BC,CD∥BE,且CD=BE.