题目内容
20.用配方法解一元二次方程2x2-5x+2=0,请结合题意填空,完成本题的解答解:方程变形为2x2-5x+($\frac{5}{2}$)2-($\frac{5}{2}$)2+2=0…第一步
配方,得(2x-$\frac{5}{2}$)2-$\frac{17}{4}$=0…第二步
移项,得(2x-$\frac{5}{2}$)2=$\frac{17}{4}$…第三步
两边开平方,得2x-$\frac{5}{2}$=±$\frac{\sqrt{17}}{2}$…第四步
即2x-$\frac{5}{2}$=$\frac{\sqrt{17}}{2}$,或2x-$\frac{5}{2}$=-$\frac{\sqrt{17}}{2}$…第五步
所以x1=$\frac{5+\sqrt{17}}{4}$,x2=$\frac{5-\sqrt{17}}{4}$…第六步
(1)上述解法错在第一步.
(2)请你用配方法求出该方程的解.
分析 (1)根据配方法的步骤即可判断;
(2)移项后将二次项系数化为1,再配上一次项系数一半的平方即可得.
解答 解:(1)上述解法错在第一步,
故答案为:一;
(2)∵2x2-5x=-2,
∴x2-$\frac{5}{2}$x=-1,
则x2-$\frac{5}{2}$x+$\frac{25}{16}$=-1+$\frac{25}{16}$,即(x-$\frac{5}{4}$)2=$\frac{9}{16}$,
∴x-$\frac{5}{4}$=±$\frac{3}{4}$,
∴x=$\frac{5}{4}$±$\frac{3}{4}$,
即x1=2,x2=$\frac{1}{2}$.
点评 本题主要考查解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.

练习册系列答案
相关题目
10.在有理式$\frac{x}{3}$、$\frac{3}{x}$、$\frac{1}{2}$(m+n)、$\frac{2x}{π-1}$、$\frac{m-n}{m+n}$中,分式有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10. 如图是小明作线段AB的垂直平分线的作法及作图痕迹,则四边形ADBC一定是( )
如图是小明作线段AB的垂直平分线的作法及作图痕迹,则四边形ADBC一定是( )
 如图是小明作线段AB的垂直平分线的作法及作图痕迹,则四边形ADBC一定是( )
如图是小明作线段AB的垂直平分线的作法及作图痕迹,则四边形ADBC一定是( )| A. | 矩形 | B. | 菱形 | C. | 正方形 | D. | 无法确定 |
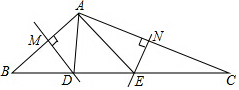 如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.