题目内容

16．已知关于x的方程2x2+（k-2）x+1=0有两个相等的实数根，求k的值．

分析 根据方程的系数结合根的判别式即可得出关于k的一元二次方程，解之即可求出k值．

解答 解：∵方程2x2+（k-2）x+1=0有两个相等的实数根，
∴△=（k-2）2-4×2×1=k2-4k-4=0，
解得：k1=2+2$\sqrt{2}$，k2=2-2$\sqrt{2}$．

点评 本题考查了根的判别式以及解一元二次方程，熟练掌握“当△=0时，方程有两个相等的两个实数根”是解题的关键．

练习册系列答案
相关题目
6．已知某种产品的进价为每件40元，现在的售价为每件60元，每星期可卖出200件，市场调查发现，该产品每降价1元，每星期可多卖出20件，由于供货方的原因销量不得超过280件，设这种产品每件降价x元，每星期的销售利润为w元．
（1）求w与x之间的函数关系式，并写出自变量x的取值范围；
（2）该产品销售价定为每件为多少元时，每星期的销售利润最大？最大利润是多少元？
（3）设该产品的售价为m元，则m在什么范围时，每星期的销售利润不低于3420元，请直接写出结果56≤m≤60．
7．求：（19932000+19952001）×31001×71002×131003计算结果的个位数字．
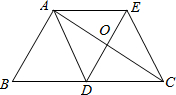4．如图，在△ABC中，AD是△ABC的中线，过点A作AE∥BC与AB的平行线DE交于点E，DE与AC相交于点O，连接EC．
（1）求证：AD∥EC；
（2）当△ABC满足条件∠BAC=90°时，四边形ADCE是菱形，请补充条件并证明．
11．（1）计算：$\frac{{x}^{2}+2x-4}{x-2}$+$\frac{{x}^{2}}{2-x}$
（2）先化简，再求值：$\frac{a-2}{{a}^{2}-1}$÷（a-1-$\frac{2a-1}{a+1}$），其中a=$\frac{1}{2}$．
1．（1）计算：$\sqrt{27}$-2cos30°+（$\sqrt{3}$）0-（-$\frac{1}{3}$）-1；
（2）解不等式组．$\left\{\begin{array}{l}\frac{x}{2}-2＜1\\ 3x+2≤4x-1\end{array}\right.$．
8．计算：
（1）（π-$\sqrt{10}$）0-$\sqrt{12}$+|-2$\sqrt{3}$|+$\sqrt{（-3）^{2}}$
（2）（$\sqrt{6}$-2$\sqrt{15}$）×$\sqrt{3}$-6$\sqrt{\frac{1}{2}}$．
5．关于x的一元二次方程x2-（k-1）x-k-1=0
（1）求证：无论x取何值，方程总有两个不相等的实数根．
（2）若方程的两根为x1、x2，是否存在这样的k值，使方程的两根的平方和为2，若存在，求出这样的k值；若不存在，请说明理由．
6．若（a-3）2+|b-4|=0，则（a-b）2004的值是（　　）
A．-1B．1C．0D．2016

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网