题目内容
 在矩形ABCD中,AB=2cm,BC=3cm,M为BC的中点.求∠DAM的度数(精确到0.1°).
在矩形ABCD中,AB=2cm,BC=3cm,M为BC的中点.求∠DAM的度数(精确到0.1°).考点:解直角三角形
专题:计算题
分析:先根据矩形的性质得到∠B=90°,AD∥BC,则∠DAM=∠AMB,然后在Rt△ABM中,利用正切的定义计算出tan∠AMB=
,再查表得到∠AMB≈53.1°,即∠DAM的度数为53.1°.
| 4 |
| 3 |
解答:解:∵四边形ABCD为矩形,
∴∠B=90°,AD∥BC,
∴∠DAM=∠AMB,
∵BC=3cm,M为BC的中点,
∴BM=
,
在Rt△ABM中,tan∠AMB=
=
=
,
∴∠AMB≈53.1°,
∴∠DAM的度数为53.1°.
∴∠B=90°,AD∥BC,
∴∠DAM=∠AMB,
∵BC=3cm,M为BC的中点,
∴BM=
| 3 |
| 2 |
在Rt△ABM中,tan∠AMB=
| AB |
| BM |
| 2 | ||
|
| 4 |
| 3 |
∴∠AMB≈53.1°,
∴∠DAM的度数为53.1°.
点评:本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.

练习册系列答案
相关题目
 如图,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,请按照图中所标注的数据计算图中实线所围成的图形的面积S是( )
如图,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,请按照图中所标注的数据计算图中实线所围成的图形的面积S是( )| A、30 | B、50 | C、60 | D、80 |
 如图,在△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠CFE为
如图,在△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠CFE为 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AD=6
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AD=6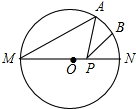 如图,MN是⊙O的直径,MN=2,点A在⊙O上,∠AMN=40°,B为弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为
如图,MN是⊙O的直径,MN=2,点A在⊙O上,∠AMN=40°,B为弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为