题目内容
如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于点D，AD=6| 3 |
| 3 |
考点：解直角三角形
专题：
分析：由条件可知∠A=∠BCD，可知sin∠A=sin∠BCD，即
=
，且AB=AD+BD，代入可求得BD，再利用勾股定理可求得AC，再利用三角函数求出∠A和∠B即可．
| BD |
| BC |
| BC |
| AB |
解答：解：∵∠ACB=90°，CD⊥AB，
∴∠A+∠ACD=∠ACD+∠BCD，
∴∠A=∠BCD，
∴sin∠A=sin∠BCD，即
=
，且AB=AD+BD，
∴
=
，整理可得BD2+6
BD-48=0，
解得BD=2
（-8
不合题意舍去），
∴AB=AD+BD=8
，
在Rt△ABC中，由勾股定理可求得AC=12，
∴sinA=
=
=
，
∴∠A=30°，∠B=90°-∠A=60°，
综上可知在Rt△ABC中，AB=8
，AC=12，∠A=30°，∠B=60°．
∴∠A+∠ACD=∠ACD+∠BCD，
∴∠A=∠BCD，
∴sin∠A=sin∠BCD，即
| BD |
| BC |
| BC |
| AB |
∴
| BD | ||
4
|
4
| ||
6
|
| 3 |
解得BD=2
| 3 |
| 3 |
∴AB=AD+BD=8
| 3 |
在Rt△ABC中，由勾股定理可求得AC=12，
∴sinA=
| BC |
| AB |
4
| ||
8
|
| 1 |
| 2 |
∴∠A=30°，∠B=90°-∠A=60°，
综上可知在Rt△ABC中，AB=8
| 3 |
点评：本题主要考查三角函数的定义及勾股定理的应用，掌握三角函数的定义及特殊角的三角函数值是解题的关键．
练习册系列答案
相关题目
在矩形ABCD中，AB=2cm，BC=3cm，M为BC的中点．求∠DAM的度数（精确到0.1°）．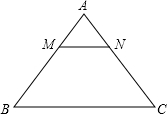
如图，已知一个等腰三角形纸片ABC，其中BC=6，AB=AC=5，M为AB上一动点（点M与点A、B不重合），过点M作MN∥BC，交AC于点N，在△AMN中，设MN的长为x，MN上的高为h．