题目内容
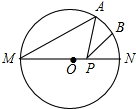如图，MN是⊙O的直径，MN=2，点A在⊙O上，∠AMN=40°，B为弧AN的中点，P是直径MN上一动点，则PA+PB的最小值为考点：轴对称-最短路线问题,勾股定理,垂径定理
专题：
分析：首先利用在直线L上的同侧有两个点A、B，在直线L上有到A、B的距离之和最短的点存在，可以通过轴对称来确定，即作出其中一点关于直线L的对称点，对称点与另一点的连线与直线L的交点就是所要找的点P的位置，然后根据弧的度数发现一个等腰直角三角形计算．
解答：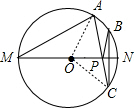
解：作点B关于MN的对称点C，连接AC交MN于点P，则P点就是所求作的点．
此时PA+PB最小，且等于AC的长．
连接OA，OC，
∵∠AMN=40°，
∴∠AON=80°，
∴
的度数是80°，
则
的度数是40°，
根据垂径定理得
的度数是40°，
则∠AOC=120°，
∵MN=2
∴OA=OC=1，
∴∠OAC=∠OCA=30°，
∴AC=
．
故答案为
．
解：作点B关于MN的对称点C，连接AC交MN于点P，则P点就是所求作的点．此时PA+PB最小，且等于AC的长．
连接OA，OC，
∵∠AMN=40°，
∴∠AON=80°，
∴
 |
| AN |
则
|
| BN |
根据垂径定理得
|
| CN |
则∠AOC=120°，
∵MN=2
∴OA=OC=1，
∴∠OAC=∠OCA=30°，
∴AC=
| 3 |
故答案为
| 3 |
点评：此题主要考查了轴对称-最短路线问题，垂径定理，直角三角形的性质等，确定点P的位置是本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
二次函数y=ax2+bx+c（a≠0）的图象如图，下列结论：
在矩形ABCD中，AB=2cm，BC=3cm，M为BC的中点．求∠DAM的度数（精确到0.1°）．下列图形中对称轴最多的是（ ）
| A、圆 | B、正方形 | C、角 | D、线段 |
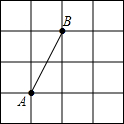如图所示，在4×4的方格中每个小正方形的边长是单位1，小正方形的顶点称为格点．现有格点A、B，在方格中任意找一点C（必须是格点），使△ABC成为等腰三角形．这样的格点有