题目内容
2. 如图,已知:DE⊥AC于E,BC⊥AC,CD⊥AB于D,∠1=∠2,说明:GF⊥AB.
如图,已知:DE⊥AC于E,BC⊥AC,CD⊥AB于D,∠1=∠2,说明:GF⊥AB.
分析 先证明DE∥BC,结合平行线的性质可得到∠1=∠3,可证明CD∥FG,可证得结论.
解答 解:∵DE⊥AC,BC⊥AC,
∴∠AED=∠ACB=90°,
∴DE∥BC,
∴∠2=∠3,
∵∠1=∠2,
∴∠1=∠3,
∴FG∥DC,
∴∠BFG=∠BDC,
∵CD⊥AB,
∴∠BDC=90°,
∴∠BFG=90°,
∴GF⊥AB.
点评 本题主要考查平行线的判定和性质,掌握平行线的判定和性质是解题的关键,①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角相等?两直线平行,④a∥b,b∥c⇒a∥c.

练习册系列答案
相关题目
13.一次函数y=-x+2图象经过( )象限.
| A. | 一、二、三 | B. | 一、二、四 | C. | 一、三、四 | D. | 二、三、四 |
7.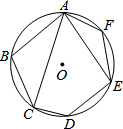 如图,在⊙O的内接六边形ABCDEF中,∠CAE=80°,则∠B+∠F的度数为( )
如图,在⊙O的内接六边形ABCDEF中,∠CAE=80°,则∠B+∠F的度数为( )
 如图,在⊙O的内接六边形ABCDEF中,∠CAE=80°,则∠B+∠F的度数为( )
如图,在⊙O的内接六边形ABCDEF中,∠CAE=80°,则∠B+∠F的度数为( )| A. | 220° | B. | 240° | C. | 260° | D. | 280° |
14. 如图,平行四边形ABCD中,AE平分∠DAB,∠B=110°,则∠DEA等于( )
如图,平行四边形ABCD中,AE平分∠DAB,∠B=110°,则∠DEA等于( )
 如图,平行四边形ABCD中,AE平分∠DAB,∠B=110°,则∠DEA等于( )
如图,平行四边形ABCD中,AE平分∠DAB,∠B=110°,则∠DEA等于( )| A. | 110° | B. | 80° | C. | 55° | D. | 35° |
11.在下列实数$\frac{22}{7}$,3.14159265,$\sqrt{8}$,-8,$\root{3}{9}$,$\sqrt{36}$,1.103 030 030 003…(两个3之间依次多一个0),$\frac{π}{3}$中,无理数有( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
12.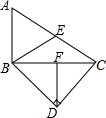 如图,在四边形ABDC中,∠BDC=90°,AB⊥BC,E、F分别是AC、BC的中点,BE、DF的大小关系是( )
如图,在四边形ABDC中,∠BDC=90°,AB⊥BC,E、F分别是AC、BC的中点,BE、DF的大小关系是( )
 如图,在四边形ABDC中,∠BDC=90°,AB⊥BC,E、F分别是AC、BC的中点,BE、DF的大小关系是( )
如图,在四边形ABDC中,∠BDC=90°,AB⊥BC,E、F分别是AC、BC的中点,BE、DF的大小关系是( )| A. | BE>DF | B. | BE=DF | C. | BE<DF | D. | 无法确定 |
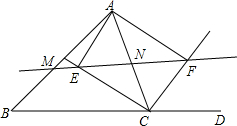 已知,如图,△ABC中,CE、CF分别是∠ACB和它的邻补角∠ACD的平分线,AE⊥CE于E,AF⊥CF于F,直线EF分别交AB、AC于M、N.
已知,如图,△ABC中,CE、CF分别是∠ACB和它的邻补角∠ACD的平分线,AE⊥CE于E,AF⊥CF于F,直线EF分别交AB、AC于M、N. …,请仔细观察,按此规律在前8个图案中有2个
…,请仔细观察,按此规律在前8个图案中有2个 ,按此规律在前15个图案中有4个
,按此规律在前15个图案中有4个 ,按此规律在前2015个图案中有503个
,按此规律在前2015个图案中有503个