题目内容
2.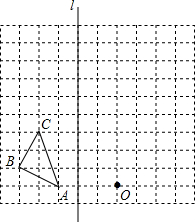 如图在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC、直线l和格点O.
如图在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC、直线l和格点O.(1)画出△ABC关于直线l成轴对称的△A0B0C0;
(2)画出将△A0B0C0向上平移1个单位得到的△A1B1C1;
(3)以格点O为位似中心,将△A1B1C1作位似变换,将其放大到原来的两倍,得到△A2B2C2.
分析 (1)利用轴对称图形的性质分别得出对应点位置进而得出答案;
(2)直接利用平移的性质进而得出对应点位置进而得出答案;
(3)直接利用位似图形的性质得出对应点位置进而得出答案.
解答  解:(1)如图所示:△A0B0C0,即为所求;
解:(1)如图所示:△A0B0C0,即为所求;
(2)如图所示:△A1B1C1,即为所求;
(3)如图所示:△A2B2C2,即为所求.
点评 此题主要考查了位似变换以及轴对称变换以及平移变换,根据题意得出对应点位置是解题关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
12.某射击队要从四名运动员中选拔一名运动员参加比赛,选拔赛中每名队员的平均成绩$\overline{x}$与方差S2如下表所示,如果要选择一个成绩高且发挥稳定的人参赛,则应该选( )
| 选手 | 甲 | 乙 | 丙 | 丁 |
| 平均数$\overline{x}$ | 8.5 | 9 | 9 | 8.5 |
| 方差S2 | 1 | 1.2 | 1 | 1.3 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
17.为了更好地迎接庐阳区排球比赛,某校积极准备,从全校学生中遴选出21名同学进行相应的排球训练,该训练队成员的身高如下表:
则该校排球队21名同学身高的众数和中位数分别是(单位:cm)( )
| 身高(cm) | 170 | 172 | 175 | 178 | 180 | 182 | 185 |
| 人数(个) | 2 | 4 | 5 | 2 | 4 | 3 | 1 |
| A. | 185,178 | B. | 178,175 | C. | 175,178 | D. | 175,175 |
14.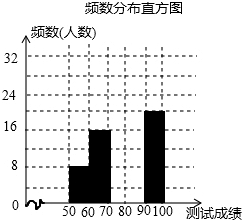 苏州某中学为了迎接第53届世乒赛,在九年级举行了“乒乓球知识竞赛”,从全年级600名学生的成绩中随机抽选了100名学生的成绩,根据测试成绩绘制成以下不完整的频数分布表和频数分布直方图:
苏州某中学为了迎接第53届世乒赛,在九年级举行了“乒乓球知识竞赛”,从全年级600名学生的成绩中随机抽选了100名学生的成绩,根据测试成绩绘制成以下不完整的频数分布表和频数分布直方图:
频率分布表:
请结合图表完成下列各题:
(1)求表中a的值:
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于90分的同学可以获得第53届世乒赛吉祥物“乒宝”,请你估计该校九年级有多少位同学可以获得“乒宝”
 苏州某中学为了迎接第53届世乒赛,在九年级举行了“乒乓球知识竞赛”,从全年级600名学生的成绩中随机抽选了100名学生的成绩,根据测试成绩绘制成以下不完整的频数分布表和频数分布直方图:
苏州某中学为了迎接第53届世乒赛,在九年级举行了“乒乓球知识竞赛”,从全年级600名学生的成绩中随机抽选了100名学生的成绩,根据测试成绩绘制成以下不完整的频数分布表和频数分布直方图:频率分布表:
| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 50≤x<60 | 8 |
| 第2组 | 60≤x<70 | 16 |
| 第3组 | 70≤x<80 | a |
| 第4组 | 80≤x<90 | 32 |
| 第5组 | 90≤x<100 | 20 |
(1)求表中a的值:
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于90分的同学可以获得第53届世乒赛吉祥物“乒宝”,请你估计该校九年级有多少位同学可以获得“乒宝”
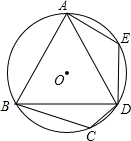 如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=110°.若点E在$\widehat{AD}$上,则∠E=125°.
如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=110°.若点E在$\widehat{AD}$上,则∠E=125°.