题目内容
10．先化简，再求值：$\frac{{m}^{2}-8m+16}{{m}^{2}+2m}$÷（m-2-$\frac{12}{m+2}$），其中m是方程$\frac{m-1}{2}=\frac{m+2}{5}$的解．分析 先将括号内部分加减，将除法转化为乘法后约分，然后将方程$\frac{m-1}{2}=\frac{m+2}{5}$的解代入求值即可．
解答 解：原式=$\frac{（m-4）^{2}}{m（m+2）}$÷（$\frac{{m}^{2}-4}{m+2}$-$\frac{12}{m+2}$）
=$\frac{{（m-4）}^{2}}{m（m+2）}$÷$\frac{{m}^{2}-16}{m+2}$
=$\frac{{（m-4）}^{2}}{m（m+2）}$•$\frac{m+2}{（m-4）（m+4）}$
=$\frac{m-4}{{m}^{2}+4m}$，
解方程$\frac{m-1}{2}=\frac{m+2}{5}$，
去分母得，5m-5=2m+4，
移项合并同类项得，3m=9，
系数化为1得，m=3，
当m=3时，原式=$\frac{3-4}{9+12}$=-$\frac{1}{21}$．
点评 本题考查了分式的化简求值、一元一次方程的解，熟悉因式分解是解题的关键．
练习册系列答案
相关题目
20．
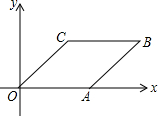菱形OABC在平面直角坐标系中的位置如图所示，∠AOC=45°，点A的坐标为（$\sqrt{2}$，0），则点B的坐标为（ ）
菱形OABC在平面直角坐标系中的位置如图所示，∠AOC=45°，点A的坐标为（$\sqrt{2}$，0），则点B的坐标为（ ）| A． | （$\sqrt{2}$，1） | B． | （1，$\sqrt{2}$） | C． | （1，$\sqrt{2}$+1） | D． | （$\sqrt{2}$+1，1） |
1．钓鱼岛自古以来就是中国的固有领土，在“百度”搜索引擎中输入“钓鱼岛最新消息”，能搜索到与之相关的结果个数约为4640000，这个数字用科学记数法表示为（ ）
| A． | 464×104 | B． | 46.4×106 | C． | 4.64×106 | D． | 0.464×107 |
学校体育运动会的颁奖台放置于校体育馆内，其主视图如图所示，则其左视图是（ ）
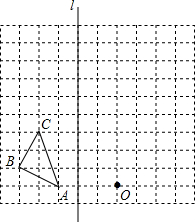如图在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC、直线l和格点O．