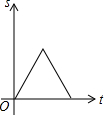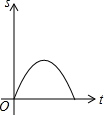题目内容
13.因式分解法解一元二次方程.$\frac{(t+3)^{2}}{5}$+1-$\frac{(3t-1)^{2}}{5}$=$\frac{t(2t-3)}{2}$.分析 首先移项,然后利用平方差公式使方程的左边进行因式分解,再进行去分母,最后解两个一元一次方程即可.
解答 解:∵$\frac{(t+3)^{2}}{5}$-$\frac{(3t-1)^{2}}{5}$=$\frac{t(2t-3)}{2}$-1,
∴$\frac{(t+3)^{2}}{5}$-$\frac{(3t-1)^{2}}{5}$=$\frac{2{t}^{2}-3t-2}{2}$,
∴$\frac{(t+3-3t+1)(t+3+3t-1)}{5}$=$\frac{(2t+1)(t-2)}{2}$,
∴$\frac{-4(t-2)(2t+1)}{5}$=$\frac{(2t+1)(t-2)}{2}$,
∴-8(t-2)(2t+1)=5(t-2)(2t+1),
∴13(t-2)(2t+1)=0,
∴t-2=0或2t+1=0,
∴t1=2,t2=-$\frac{1}{2}$.
点评 本题主要考查了因式分解法解一元二次方程的知识,解答本题的关键是熟练掌握平方差公式的应用,此题难度不大.

练习册系列答案
相关题目
1.钓鱼岛自古以来就是中国的固有领土,在“百度”搜索引擎中输入“钓鱼岛最新消息”,能搜索到与之相关的结果个数约为4640000,这个数字用科学记数法表示为( )
| A. | 464×104 | B. | 46.4×106 | C. | 4.64×106 | D. | 0.464×107 |
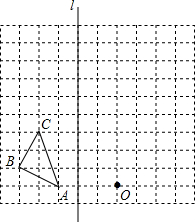 如图在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC、直线l和格点O.
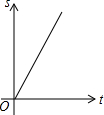
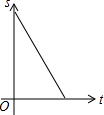
如图在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC、直线l和格点O.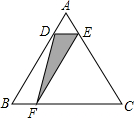 如图,在等边△ABC中,点D是AB边上的动点,过点作DE∥BC交边AC于点E,过点作EF∥AB交边BC于点F.连结DF,设动点D从点A出发沿AB匀速向点B运动,运动时间为t,则在整个运动过程中,△DEF的面积S与运动时间t的大致图象是( )
如图,在等边△ABC中,点D是AB边上的动点,过点作DE∥BC交边AC于点E,过点作EF∥AB交边BC于点F.连结DF,设动点D从点A出发沿AB匀速向点B运动,运动时间为t,则在整个运动过程中,△DEF的面积S与运动时间t的大致图象是( )