题目内容
5.解关于x的方程:(1)(2x-5)2=(x-2)2
(2)(1+x)2+(1+x)=12
(3)x2+ax+b=0(配方法)
分析 (1)直接开方法解即可.
(2)因式分解法解即可.
(3)根据配方法的步骤解即可.
解答 解:(1)∵(2x-5)2=(x-2)2
∴2x-5=±(x-2),
∴x1=3,x2=$\frac{7}{3}$.
(2)∵(1+x)2+(1+x)=12
∴(1+x)2+(1+x)-12=0
∴(1+x+4)(1+x-3)=0,
∴1+x+4=0或1+x-3=0,
∴x1=2,x2=-5.
(3)∵x2+ax+b=0,
∴x2+ax=-b
∴x2+ax+($\frac{a}{2}$)2=($\frac{a}{2}$)2-b,
∴(x+$\frac{a}{2}$)2=$\frac{{a}^{2}-4b}{4}$
当a2-4b<0时,方程无解.
当a2-4b≥0时,x=-$\frac{a}{2}$±$\frac{\sqrt{{a}^{2}-4b}}{2}$.
点评 本题考查一元二次方程的解法,解题的关键是熟练掌握一元二次方程的解法,属于基础题,中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.下列说法正确的是( )
| A. | 三点确定一个圆 | |
| B. | 经过圆心的直线是圆的对称轴 | |
| C. | 和半径垂直的直线是圆的切线 | |
| D. | 三角形的内心到三角形三个顶点距离相等 |
 如图,∠ABC=∠ADC=90°,E是AC的中点,∠BDE=32°,则∠DEB=116°.
如图,∠ABC=∠ADC=90°,E是AC的中点,∠BDE=32°,则∠DEB=116°.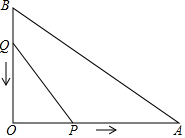 如图,在△AOB中,∠AOB=90°,OA=12cm,AB=6$\sqrt{5}$cm,点P从O开始沿OA边向点A以2cm/s(厘米/秒)的速度移动;点Q从点B开始沿BO边向点O以1cm/s的速度移动,如果P,Q同时出发,用x(秒)表示时间(0≤x≤6),那么:
如图,在△AOB中,∠AOB=90°,OA=12cm,AB=6$\sqrt{5}$cm,点P从O开始沿OA边向点A以2cm/s(厘米/秒)的速度移动;点Q从点B开始沿BO边向点O以1cm/s的速度移动,如果P,Q同时出发,用x(秒)表示时间(0≤x≤6),那么: