题目内容
14. 如图,AB,CD相交于点O,点E,F在AB上,AE=BF,AD=BC,AD∥BC.求证:OE=OF.
如图,AB,CD相交于点O,点E,F在AB上,AE=BF,AD=BC,AD∥BC.求证:OE=OF.
分析 利用已知条件证明△ADO≌△BCO,所以AO=BO,由AE=BF,所以AO-AE=BO-BF,即OE=OF.
解答 证明:∵AD∥BC,
∴∠ADO=∠BCO,
在△ADO和△BCO中,
$\left\{\begin{array}{l}{∠ADO=∠BCO}\\{∠AOD=∠BOC}\\{AD=BC}\end{array}\right.$
∴△ADO≌△BCO,
∴AO=BO,
∵AE=BF,
∴AO-AE=BO-BF,
即OE=OF.
点评 本题考查了全等三角形的性质与判定,解决本题的关键是证明△ADO≌△BCO.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.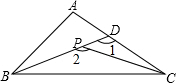 如图,P是△ABC内一点,延长CP交AB于D,则下列不等式成立的是( )
如图,P是△ABC内一点,延长CP交AB于D,则下列不等式成立的是( )
 如图,P是△ABC内一点,延长CP交AB于D,则下列不等式成立的是( )
如图,P是△ABC内一点,延长CP交AB于D,则下列不等式成立的是( )| A. | ∠2>∠A>∠1 | B. | ∠2>∠1>∠A | C. | ∠1>∠A>∠2 | D. | ∠A>∠1>∠2 |
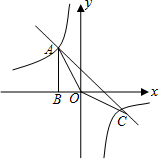 如图,Rt△ABO的顶点A是双曲线y=$\frac{k}{x}$(k≠0)与直线y=-x-(k+1)在第二象限的交点,AB⊥x轴于B,点C是双曲线与直线的另一个交点,且S△ABO=$\frac{3}{2}$.
如图,Rt△ABO的顶点A是双曲线y=$\frac{k}{x}$(k≠0)与直线y=-x-(k+1)在第二象限的交点,AB⊥x轴于B,点C是双曲线与直线的另一个交点,且S△ABO=$\frac{3}{2}$. 如图,角α的顶点为O,它的一边在x轴的正半轴上,另一边上有一点P(3,4),则sinα=$\frac{4}{5}$.
如图,角α的顶点为O,它的一边在x轴的正半轴上,另一边上有一点P(3,4),则sinα=$\frac{4}{5}$.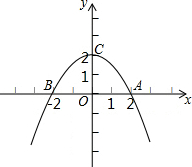 已知如图所示,抛物线y=-$\frac{1}{2}$x2+m-3与x轴交于A,B 两点.且OA=OC.求:
已知如图所示,抛物线y=-$\frac{1}{2}$x2+m-3与x轴交于A,B 两点.且OA=OC.求:
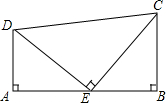 如图,已知CE=DE,∠A=∠B=CED=90°,若AB=5,BC=3,求AD的长.
如图,已知CE=DE,∠A=∠B=CED=90°,若AB=5,BC=3,求AD的长.