题目内容
4.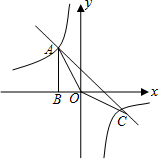 如图,Rt△ABO的顶点A是双曲线y=$\frac{k}{x}$(k≠0)与直线y=-x-(k+1)在第二象限的交点,AB⊥x轴于B,点C是双曲线与直线的另一个交点,且S△ABO=$\frac{3}{2}$.
如图,Rt△ABO的顶点A是双曲线y=$\frac{k}{x}$(k≠0)与直线y=-x-(k+1)在第二象限的交点,AB⊥x轴于B,点C是双曲线与直线的另一个交点,且S△ABO=$\frac{3}{2}$.(1)求这两个函数的解析式;
(2)直接写出使一次函数的值大于反比例函数的值的x的取值范围.
分析 (1)先根据反比例函数的图象所在的象限判断出k的符号,再由△ABO的面积求出k的值,进而可得出两个函数的解析式;
(2)先把两函数的解析式联立组成方程组,求出x、y的值,得出A、C两点的坐标,观察图象,根据一次函数与反比例函数的交点坐标即可求出一次函数的值大于反比例函数的值x的取值范围.
解答 解:(1)∵反比例函数y=$\frac{k}{x}$的图象在二、四象限,
∴k<0,
∵S△ABO=$\frac{1}{2}$|k|=$\frac{3}{2}$,
∴k=-3,
∴双曲线的解析式为:y=-$\frac{3}{x}$,
直线y=-x-(k+1)的解析式为:y=-x-(-3+1),即y=-x+2;
(2)∵把一次函数与反比例函数的解析式组成方程组,
得$\left\{\begin{array}{l}{y=-x+2}\\{y=-\frac{3}{x}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{x}_{1}=-1}\\{{y}_{1}=3}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=3}\\{{y}_{2}=-1}\end{array}\right.$,
∴A(-1,3),C(3,-1);
∵一次函数的解析式为:y=-x+2,
∴令y=0,则-x+2=0,即x=2,
∴直线AC与x轴的交点D(2,0),
∵A(-1,3),C(3,-1),
∴当x<-1或0<x<3时,一次函数的值大于反比例函数的值.
点评 此题考查了反比例函数比例系数k的几何意义,反比例函数的性质,求两函数的交点坐标,比较函数值的大小,三角形的面积等知识,能根据△ABO的面积求出k的值是解答此题的关键.

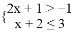 的解集表示在数轴上,下列选项正确的是( )
的解集表示在数轴上,下列选项正确的是( ) B.
B. 
 D.
D. 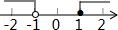
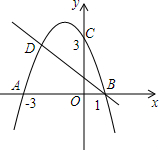 如图,二次函数的图象与x轴相交于A(-3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
如图,二次函数的图象与x轴相交于A(-3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D. 如图,把一张长方形的纸按图那样折叠后,B、D两点落在B′、D′点处,若得∠AOB′=80°,则∠B′OG的度数为50°.
如图,把一张长方形的纸按图那样折叠后,B、D两点落在B′、D′点处,若得∠AOB′=80°,则∠B′OG的度数为50°.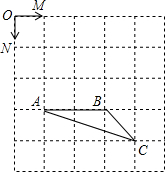 如图,已知正方形网格中每个小正方形的边长为1,点O、M、N、A、B、C都是小正方形的顶点.
如图,已知正方形网格中每个小正方形的边长为1,点O、M、N、A、B、C都是小正方形的顶点. 如图,AB,CD相交于点O,点E,F在AB上,AE=BF,AD=BC,AD∥BC.求证:OE=OF.
如图,AB,CD相交于点O,点E,F在AB上,AE=BF,AD=BC,AD∥BC.求证:OE=OF.