题目内容
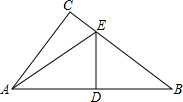 如图,在△ABC,∠C=90°,DE垂直平分斜边AB,分别交AB、BC于D、E.若∠CAE=∠B+40°,求∠AEB的度数.
如图,在△ABC,∠C=90°,DE垂直平分斜边AB,分别交AB、BC于D、E.若∠CAE=∠B+40°,求∠AEB的度数.考点:线段垂直平分线的性质
专题:
分析:利用垂直平分线的性质可得到∠B=∠EAB,结合条件在△ACB中可得∠B+40°+∠B+∠B=90°,可求得∠B,在△AEB中利用三角形内角和定理可求得∠AEB的度数.
解答:解:∵DE垂直平分斜边AB,
∴AE=BE,
∴∠B=∠EAB,
∵∠C=90°,
∴∠CAB+∠B=90°,
又∵∠CAE=∠B+40°,
∴∠B+40°+∠B+∠B=90°,
∴∠B=
,
∴∠AEB=180°-2∠B=180°-
=
.
∴AE=BE,
∴∠B=∠EAB,
∵∠C=90°,
∴∠CAB+∠B=90°,
又∵∠CAE=∠B+40°,
∴∠B+40°+∠B+∠B=90°,
∴∠B=
| 50° |
| 3 |
∴∠AEB=180°-2∠B=180°-
| 100° |
| 3 |
| 440° |
| 3 |
点评:本题主要考查线段垂直平分线的性质,利用直角三角形的两锐角互余得到关于∠B的方程求得∠B是解题的关键.

练习册系列答案
相关题目
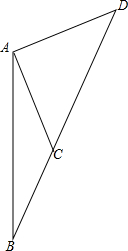 如图,距沿海某城市A的正南方向240千米B处有一台风中心,该台风中心现正以20千米/小时速度沿北偏东30°方向直线移动,当台风到达C处时,对A城市造成影响,一直到离开D处时,影响消失.已知AC=AD=200千米,问该台风影响该城市持续的时间有多长?
如图,距沿海某城市A的正南方向240千米B处有一台风中心,该台风中心现正以20千米/小时速度沿北偏东30°方向直线移动,当台风到达C处时,对A城市造成影响,一直到离开D处时,影响消失.已知AC=AD=200千米,问该台风影响该城市持续的时间有多长? 如图:一次函数y=kx+b的图象经过A、B两点,A(3,5),B(0,2),直线AB与x轴交点于C,求△AOC的面积.
如图:一次函数y=kx+b的图象经过A、B两点,A(3,5),B(0,2),直线AB与x轴交点于C,求△AOC的面积. 如图,数轴上点A表示的数是
如图,数轴上点A表示的数是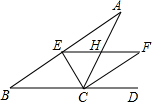 已知:如图,∠ACD是△ABC的一个外角,CE、CF分别平分∠ACB、∠ACD,EF∥BC,分别交AC、CF于点H、F.求证:EH=HF.
已知:如图,∠ACD是△ABC的一个外角,CE、CF分别平分∠ACB、∠ACD,EF∥BC,分别交AC、CF于点H、F.求证:EH=HF.