题目内容
1.已知关于x的方程x2+mx+m-3=0.(1)若该方程的一个根为2,求m的值及方程的另一个根;
(2)求证:不论m取何实数,该方程都有两个不相等的实数根.
分析 (1)把x=2代入原方程求得m的值,进一步求得方程的另一个根即可;
(2)计算出根的判别式,进一步利用配方法和非负数的性质证得结论即可.
解答 解:(1)将x=2代入方程x2+mx+m-3=0得4+2m+m-3=0,解得m=-$\frac{1}{3}$,
方程为x2-$\frac{1}{3}$x-$\frac{10}{3}$=0,即3x2-x-10=0,
解得x1=$\frac{5}{3}$,x2=-2.
(2)∵△=m2-4(m-3)
=m2-4m+12
=(m-2)2+8>0,
∴不论m取何实数,该方程都有两个不相等的实数根.
点评 此题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了一元二次方程的解的定义.

练习册系列答案
相关题目
11.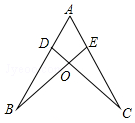 如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,有下列条件:①AB=AC;②DC=BE;③∠B=∠C,从中选择两个条件判定△ABE≌△ACD,是真命题的个数为( )
如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,有下列条件:①AB=AC;②DC=BE;③∠B=∠C,从中选择两个条件判定△ABE≌△ACD,是真命题的个数为( )
 如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,有下列条件:①AB=AC;②DC=BE;③∠B=∠C,从中选择两个条件判定△ABE≌△ACD,是真命题的个数为( )
如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,有下列条件:①AB=AC;②DC=BE;③∠B=∠C,从中选择两个条件判定△ABE≌△ACD,是真命题的个数为( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
12.若分式$\frac{x+2}{x-2}$的值为0,则x的取值应满足是( )
| A. | x=-2 | B. | x≠-2 | C. | x=2 | D. | x≠2 |
9.有一个正方体,6个面上分别标有1~6这6个整数,投掷这个正方体一次,则出现向上一面的数字为偶数的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
16.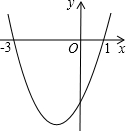 如图,二次函数y=ax2+bx+c的图象与x轴的交点的横坐标分别为-3,1,则下列结论正确的个数有( )
如图,二次函数y=ax2+bx+c的图象与x轴的交点的横坐标分别为-3,1,则下列结论正确的个数有( )
①ac>0;②2a-b=0;③4a-2b+c>0;④对于任意实数m均有am2+bm≥a-b.
 如图,二次函数y=ax2+bx+c的图象与x轴的交点的横坐标分别为-3,1,则下列结论正确的个数有( )
如图,二次函数y=ax2+bx+c的图象与x轴的交点的横坐标分别为-3,1,则下列结论正确的个数有( )①ac>0;②2a-b=0;③4a-2b+c>0;④对于任意实数m均有am2+bm≥a-b.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
10.已知一个等腰三角形两边长之比为1:4,周长为18,则这个等腰三角形底边长为( )
| A. | 2 | B. | 6 | C. | 8 | D. | 2或8 |