题目内容
14.计算(1)-t3•(-t)4•(-t)5
(2)(3a3)3+a3•a6-3a9
(3)${(2\frac{1}{3})^{200}}•{(\frac{3}{7})^{201}}$
(4)(p-q)4÷(q-p)3•(p-q)2.
分析 (1)根据同底数幂的乘法进行计算即可;
(2)根据幂的乘方、同底数幂的乘法、合并同类项进行计算即可;
(3)根据积的乘方进行计算即可;
(4)根据同底数幂的乘方进行计算即可.
解答 解:(1)-t3•(-t)4•(-t)5
=t3+4+5
=t12;
(2)(3a3)3+a3•a6-3a9
=27a9+a9-3a9
=25a9;
(3)${(2\frac{1}{3})^{200}}•{(\frac{3}{7})^{201}}$
=$(\frac{7}{3})^{200}•(\frac{3}{7})^{201}$
=$(\frac{7}{3}×\frac{3}{7})^{200}×\frac{3}{7}$
=$\frac{3}{7}$;
(4)(p-q)4÷(q-p)3•(p-q)2.
=-(p-q)4÷(p-q)3•(p-q)2
=-(p-q)4-3+2
=-(p-q)3.
点评 本题考查整式的混合运算,解题的关键是明确整式的混合运算的计算方法.

练习册系列答案
相关题目
9.下列图形中,把△ABC平移后,能得到△DEF的是( )
| A. |  | B. |  | C. |  | D. |  |
6. 如图,△ABC中,AD⊥BC于点D,BE平分∠ABC,若∠ABC=64°,∠AEB=70°.
如图,△ABC中,AD⊥BC于点D,BE平分∠ABC,若∠ABC=64°,∠AEB=70°.
(1)求∠CAD的度数;
(2)若点F为线段BC上的任意一点,当△EFC为直角三角形时,求∠BEF的度数.
 如图,△ABC中,AD⊥BC于点D,BE平分∠ABC,若∠ABC=64°,∠AEB=70°.
如图,△ABC中,AD⊥BC于点D,BE平分∠ABC,若∠ABC=64°,∠AEB=70°.(1)求∠CAD的度数;
(2)若点F为线段BC上的任意一点,当△EFC为直角三角形时,求∠BEF的度数.
3.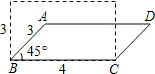 如图,矩形的长和宽分别是4和3,当矩形被“压扁”成内角为45°的平行四边形时,面积大约变成了原来的( )
如图,矩形的长和宽分别是4和3,当矩形被“压扁”成内角为45°的平行四边形时,面积大约变成了原来的( )
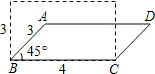 如图,矩形的长和宽分别是4和3,当矩形被“压扁”成内角为45°的平行四边形时,面积大约变成了原来的( )
如图,矩形的长和宽分别是4和3,当矩形被“压扁”成内角为45°的平行四边形时,面积大约变成了原来的( )| A. | 50% | B. | 60% | C. | 70% | D. | 80% |
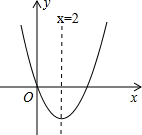 二次函数y=x2+bx的图象如图所示,对称轴为x=2,若关于x的一元二次方程x2+bx-t=0(t为实数)在-1<x<6的范围内无解,则t的取值范围是t<-4或t≥12.
二次函数y=x2+bx的图象如图所示,对称轴为x=2,若关于x的一元二次方程x2+bx-t=0(t为实数)在-1<x<6的范围内无解,则t的取值范围是t<-4或t≥12.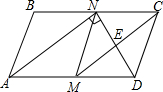 如图,在平行四边形ABCD中,M,N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点E.
如图,在平行四边形ABCD中,M,N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点E.