题目内容
19.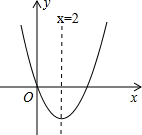 二次函数y=x2+bx的图象如图所示,对称轴为x=2,若关于x的一元二次方程x2+bx-t=0(t为实数)在-1<x<6的范围内无解,则t的取值范围是t<-4或t≥12.
二次函数y=x2+bx的图象如图所示,对称轴为x=2,若关于x的一元二次方程x2+bx-t=0(t为实数)在-1<x<6的范围内无解,则t的取值范围是t<-4或t≥12.
分析 根据抛物线的对称轴方程可求出抛物线的解析式,要使关于x的一元二次方程x2+bx-t=0(t为实数)在-1<x<6的范围内无解,只需直线y=t与抛物线y=x2+bx在-1<x<6的范围内没有交点,只需结合图象就可解决问题.
解答 解:∵抛物线y=x2+bx的对称轴为x=2,
∴x=-$\frac{b}{2}$=2,
∴b=-4,
∴抛物线的解析式为y=x2-4x.
当x=-1时,y=5;
当x=2时y=-4;
当x=6时y=12.
结合图象可得:
当t<-4或t≥12时,直线y=t与抛物线y=x2-4x在-1<x<6的范围内没有交点,
即关于x的一元二次方程x2-4x-t=0(t为实数)在-1<x<6的范围内无解.
故答案为t<-4或t≥12.
点评 本题主要考查了抛物线的性质、抛物线上点的坐标特征等知识,运用数形结合的思想是解决本题的关键.

练习册系列答案
相关题目
10. 如图,点O在直线AB上,CO⊥DO,垂足为O,则∠1与∠2的度数和为( )
如图,点O在直线AB上,CO⊥DO,垂足为O,则∠1与∠2的度数和为( )
 如图,点O在直线AB上,CO⊥DO,垂足为O,则∠1与∠2的度数和为( )
如图,点O在直线AB上,CO⊥DO,垂足为O,则∠1与∠2的度数和为( )| A. | 45° | B. | 60° | C. | 90° | D. | 无法确定 |
4.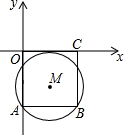 如图,在平面直角坐标系中,正方形ABCO的顶点A、C分别在y轴、x轴上,以AB为弦的⊙M与x轴相切,若点A的坐标为(0,-4),则圆心M的坐标为( )
如图,在平面直角坐标系中,正方形ABCO的顶点A、C分别在y轴、x轴上,以AB为弦的⊙M与x轴相切,若点A的坐标为(0,-4),则圆心M的坐标为( )
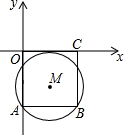 如图,在平面直角坐标系中,正方形ABCO的顶点A、C分别在y轴、x轴上,以AB为弦的⊙M与x轴相切,若点A的坐标为(0,-4),则圆心M的坐标为( )
如图,在平面直角坐标系中,正方形ABCO的顶点A、C分别在y轴、x轴上,以AB为弦的⊙M与x轴相切,若点A的坐标为(0,-4),则圆心M的坐标为( )| A. | (-2,2.5) | B. | (2,-1.5) | C. | (2.5,-2) | D. | (2,-2.5) |
8.2013年12月2日凌晨,我国长征系列火箭中运载能力最强的“大力士”--长三乙增强型火箭将3780公斤重的“嫦娥三号”精准地送入远地点380000公里的地月转移轨道.380000用科学记数法表示为( )
| A. | 3.8×104 | B. | 3.8×105 | C. | 0.38×105 | D. | 0.38×104 |
 周末,墨墨用6个相同的小正方体积木搭成了如图所示的几何体,当从左边看这个几何体时,看到的图形应是( )
周末,墨墨用6个相同的小正方体积木搭成了如图所示的几何体,当从左边看这个几何体时,看到的图形应是( )



 如图,直线l上有A、B两点,AB=24cm,点O是线段AB上的一点,OA=2OB.
如图,直线l上有A、B两点,AB=24cm,点O是线段AB上的一点,OA=2OB.