题目内容
4. 如图.已知⊙O1和⊙O2相交于A、B两点.且O1在⊙O2上,O2在⊙O1上.求∠O1AB的度数.
如图.已知⊙O1和⊙O2相交于A、B两点.且O1在⊙O2上,O2在⊙O1上.求∠O1AB的度数.
分析 如图,连接O1O2,AO2,BO1,BO2.先证明△AO1O2,△BO1O2是等边三角形,四边形AO1BO2是菱形,由此即可解决问题.
解答  解:如图,连接O1O2,AO2,BO1,BO2.
解:如图,连接O1O2,AO2,BO1,BO2.
∵O1O2=AO2=BO1=BO2=AO1,
∴△AO1O2,△BO1O2都是等边三角形,四边形AO1BO2是菱形,
∴∠O1AO2=60°,
∴∠O1AB=$\frac{1}{2}$∠O1AO2=30°.
点评 本题考查相交两个圆的性质、等边三角形的判定和性质、菱形的判定和性质等知识,解题的关键是添加辅助线,构造等边三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
4.下列计算正确的是( )
| A. | $\sqrt{2}$×$\sqrt{5}$=$\sqrt{10}$ | B. | x8÷x2=x4 | C. | (2a)3=6a3 | D. | 3a5•2a3=6a6 |
9.将一张大小为10cm×10cm的正方形纸片,依下图所示方式折叠并剪裁后再展开,其中折线(虚线)正好过三角形两边的中点,则展开后内部的正方形(无阴影部分)面积等于( )


| A. | 25cm2 | B. | 50cm2 | C. | 75cm2 | D. | 40cm |
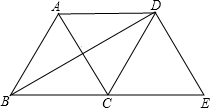 如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:
如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论: