题目内容
3.在△ABC中,AB=AC=17cm,BC=16cm,AD是角平分线,则△ABC的面积为120cm2.分析 由等腰三角形的性质得出AD⊥BC,BD=CD=$\frac{1}{2}$BC=8cm,由勾股定理求出AD,△ABC的面积=$\frac{1}{2}$BC•AD,即可得出结果.
解答 解:∵AB=AC=17cm,AD是角平分线,
∴AD⊥BC,BD=CD=$\frac{1}{2}$BC=8cm,
∴∠ADB=90°,
由勾股定理得:AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{1{7}^{2}-{8}^{2}}$=15(cm),
∴△ABC的面积=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×16×15=120(cm2);
故答案为:120.
点评 本题考查了等腰三角形的性质、勾股定理、三角形面积的计算方法;熟练掌握等腰三角形的性质,运用勾股定理求出AD是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.据报道,2016年深圳双创活动周上会场参观人数累计超过50万人,某数学学习兴趣小组为了解参观者的职业情况,他们应采用的收集数据的方式是( )
| A. | 对所有参观者发放问卷进行调查 | |
| B. | 对所有参观者中的成年人发放问卷进行调查 | |
| C. | 在主会场入口随机发放问卷进行调查 | |
| D. | 在无人机展厅随机发放问卷进行调查 |
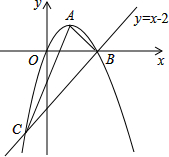 如图,已知抛物线经过原点O,顶点为A(1,1),且与直线y=x-2交于B,C两点.
如图,已知抛物线经过原点O,顶点为A(1,1),且与直线y=x-2交于B,C两点.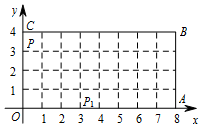 如图,动点P从(0,3)出发,沿所示方向运动,每当碰到长方形OABC的边时反弹,反弹时反射角等于入射角,记点P第1次碰到矩形的边时的点为P1(3,0),第2次碰到长方形的边时的点为P2(7,4),以此类推,则点P2014的坐标为( )
如图,动点P从(0,3)出发,沿所示方向运动,每当碰到长方形OABC的边时反弹,反弹时反射角等于入射角,记点P第1次碰到矩形的边时的点为P1(3,0),第2次碰到长方形的边时的点为P2(7,4),以此类推,则点P2014的坐标为( ) 在△ABC中,AD是中线,已知△ADC的周长比△ABD的周长多5cm,AB长为3cm.求AC的长.
在△ABC中,AD是中线,已知△ADC的周长比△ABD的周长多5cm,AB长为3cm.求AC的长. 如图,△ABC中,∠ACB=90°,D为AB中点,BC=6,CD=5,则△ABC的面积等于24.
如图,△ABC中,∠ACB=90°,D为AB中点,BC=6,CD=5,则△ABC的面积等于24.