题目内容
8. 如图,线段AD,BC相交于点O,已知OA=4,OB=3,OC=9,OD=12,C,D,E三点在一直线上,求证:∠A+∠EDO=180°.
如图,线段AD,BC相交于点O,已知OA=4,OB=3,OC=9,OD=12,C,D,E三点在一直线上,求证:∠A+∠EDO=180°.
分析 根据$\frac{OA}{OD}=\frac{OB}{OC}$,∠AOB=∠DOC,于是得到△ABO∽△DCO,根据相似三角形的性质得到∠B=∠C,证得AB∥CD,根据平行线的性质即可得到结论.
解答 解:∵OA=4,OB=3,OC=9,OD=12,
∴$\frac{OA}{OD}$=$\frac{4}{12}$=$\frac{1}{3}$,$\frac{OB}{OC}$=$\frac{3}{9}$=$\frac{1}{3}$,
∴$\frac{OA}{OD}=\frac{OB}{OC}$,
∵∠AOB=∠DOC,
∴△ABO∽△DCO,
∴∠B=∠C,
∴AB∥CD,
∴∠A+∠EDO=180°.
点评 本题考查了相似三角形的判定和性质,平行线的判定和性质,熟练掌握各定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.下列说法正确的是( )
| A. | 不相交的两条直线是平行线 | |
| B. | 经过一点有且只有一条直线与已知直线平行 | |
| C. | 若直线a平行于直线b,直线b平行于直线c,则直线a平行于直线c | |
| D. | 没有公共点的两条直线平行 |
20.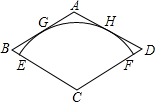 在菱形ABCD中,∠A=120°,AB=2$\sqrt{3}$,以点C为圆心的弧$\widehat{EF}$,分别与AB、AD相切于G、H,与BC、CD分别相交于点E、F,用扇形CEF做成圆锥的侧面,则圆锥的底面圆的半径为( )
在菱形ABCD中,∠A=120°,AB=2$\sqrt{3}$,以点C为圆心的弧$\widehat{EF}$,分别与AB、AD相切于G、H,与BC、CD分别相交于点E、F,用扇形CEF做成圆锥的侧面,则圆锥的底面圆的半径为( )
 在菱形ABCD中,∠A=120°,AB=2$\sqrt{3}$,以点C为圆心的弧$\widehat{EF}$,分别与AB、AD相切于G、H,与BC、CD分别相交于点E、F,用扇形CEF做成圆锥的侧面,则圆锥的底面圆的半径为( )
在菱形ABCD中,∠A=120°,AB=2$\sqrt{3}$,以点C为圆心的弧$\widehat{EF}$,分别与AB、AD相切于G、H,与BC、CD分别相交于点E、F,用扇形CEF做成圆锥的侧面,则圆锥的底面圆的半径为( )| A. | 2 | B. | $\frac{1}{2}$ | C. | $\sqrt{3}$ | D. | 1 |
18.在平面直角坐标系中,若点P关于x轴的对称点在第二象限,且到x轴的距离为2,到y轴的距离为3,则点P的坐标为( )
| A. | (-3,-2) | B. | (-2,-3) | C. | (2,3) | D. | (3,2) |
 如图,直线l:y=kx+b经过A(0,-1)、B(1,0)两点,则关于x的不等式kx+b>0的解集为x>1.
如图,直线l:y=kx+b经过A(0,-1)、B(1,0)两点,则关于x的不等式kx+b>0的解集为x>1. 如图所示,以?ABCD的顶点A为圆心,AB为半径作圆,分别交AD,BC于点E,F,延长BA交⊙A于G.
如图所示,以?ABCD的顶点A为圆心,AB为半径作圆,分别交AD,BC于点E,F,延长BA交⊙A于G.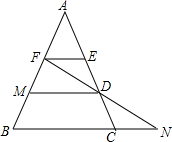 已知,如图在△ABC中,AE=ED=DC,FE∥MD∥BC,FD的延长线交BC的延长线于N,则$\frac{EF}{BN}$为$\frac{1}{4}$.
已知,如图在△ABC中,AE=ED=DC,FE∥MD∥BC,FD的延长线交BC的延长线于N,则$\frac{EF}{BN}$为$\frac{1}{4}$.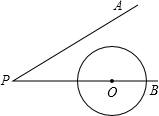 如图,∠APB=30°⊙O半径为1cm,圆心O在PB上,OP=3cm,若⊙O沿BP方向移动,当⊙O与直线PA相切时,圆心O移动的距离为1或5cm.
如图,∠APB=30°⊙O半径为1cm,圆心O在PB上,OP=3cm,若⊙O沿BP方向移动,当⊙O与直线PA相切时,圆心O移动的距离为1或5cm.