题目内容
17.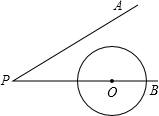 如图,∠APB=30°⊙O半径为1cm,圆心O在PB上,OP=3cm,若⊙O沿BP方向移动,当⊙O与直线PA相切时,圆心O移动的距离为1或5cm.
如图,∠APB=30°⊙O半径为1cm,圆心O在PB上,OP=3cm,若⊙O沿BP方向移动,当⊙O与直线PA相切时,圆心O移动的距离为1或5cm.
分析 当⊙O与PA相切时,切点为点C,如图所示,连接OC,根据OC的长,利用30度所对的直角边等于斜边的一半求出此时OP的长,当O移到到射线PB的反向延长线上时,分别求出圆心O移到的距离即可.
解答 解:当⊙O与PA相切时,切点为点C,如图1所示,连接OC,
∵PA为圆O的切线,
∴OC⊥PA,
在Rt△PCO中,∠APB=30°,OC=1cm,
∴OP=2OC=2,
此时圆心O移到的距离为3-2=1cm;
当P在射线PB的反向延长线上时,如图2所示,
同理圆心O移到的距离为3+2=5cm.
故答案为:1或5
点评 此题考查了直线与圆的位置关系,熟练掌握直线与圆相切的性质是解本题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
7.将二次函数y=x2的图象先向右平移2个单位,再向上平移3个单位后,所得图象的函数表达式是( )
| A. | y=(x+2)2+3 | B. | y=(x-2)2-3 | C. | y=(x-2)2+3 | D. | y=(x+2)2-3 |
9.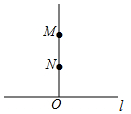 如图,已知ON⊥l,OM⊥l,所以OM与ON重合,这个推理的根据是( )
如图,已知ON⊥l,OM⊥l,所以OM与ON重合,这个推理的根据是( )
 如图,已知ON⊥l,OM⊥l,所以OM与ON重合,这个推理的根据是( )
如图,已知ON⊥l,OM⊥l,所以OM与ON重合,这个推理的根据是( )| A. | 过一点只能作一条垂线 | |
| B. | 过两点只能作一条垂线 | |
| C. | 垂线段最短 | |
| D. | 经过一点有且只有一条直线垂直于已知直线 |
 如图,线段AD,BC相交于点O,已知OA=4,OB=3,OC=9,OD=12,C,D,E三点在一直线上,求证:∠A+∠EDO=180°.
如图,线段AD,BC相交于点O,已知OA=4,OB=3,OC=9,OD=12,C,D,E三点在一直线上,求证:∠A+∠EDO=180°. 图中的几何体是由三个大小相同的正方体组成的,它的主视图为( )
图中的几何体是由三个大小相同的正方体组成的,它的主视图为( )



 如图,网格中每一个小正方形的边长为1个单位长度.
如图,网格中每一个小正方形的边长为1个单位长度.
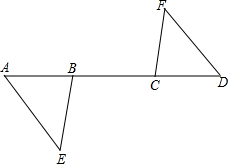 已知:如图,A,B,C,D四点在一条直线上,AC=BD,AE∥DF,∠ABE=∠DCF,求证:△ABE≌△DCF.
已知:如图,A,B,C,D四点在一条直线上,AC=BD,AE∥DF,∠ABE=∠DCF,求证:△ABE≌△DCF.